Statistical Models

Lecture 6

Dr. Silvio Fanzon
S.Fanzon@hull.ac.uk

University of Hull

Lecture 6:
Chi-squared test &
Least Squares

Outline of Lecture 6

  1. Chi-squared test of independence
  2. Worked Example
  1. Lists
  2. Data Frames
  3. Data Entry
  4. Least squares
  5. Worked Example

Part 1:
Chi-squared test
of independence

Testing for independence

Owned Rented Total
North West 2180 871 3051
London 1820 1400 3220
South West 1703 614 2317
Total 5703 2885 8588

  • Consider a two-way contingency table as above

  • To each person we associate two categories:

    • Residential Status: Rental or Owned
    • Region in which they live: NW, London, SW

Testing for independence

Owned Rented Total
North West 2180 871 3051
London 1820 1400 3220
South West 1703 614 2317
Total 5703 2885 8588
  • One possible question is:
    • Does Residential Status depend on Region?
    • In other words: Are rows and columns dependent?

Testing for independence

Owned Rented Total
North West 2180 871 3051
London 1820 1400 3220
South West 1703 614 2317
Total 5703 2885 8588
  • Looking at the data, it seems clear that:
    • London: Rentals are almost comparable to Owned
    • NW and SW: Rentals are almost a third of Owned
    • It appears Residential Status and Region are dependent features
  • Goal: Formulate test for independence

Testing for independence

Y = 1 \ldots Y = C Totals
X = 1 O_{11} \ldots O_{1C} O_{1+}
\cdots \cdots \cdots \cdots \cdots
X = R O_{R1} \ldots O_{RC} O_{R+}
Totals O_{+1} \ldots O_{+C} m

  • Consider the general two-way contingency table as above

  • They are equivalent:

    • Rows and columns are independent
    • Random variables X and Y are independent

Testing for independence

Y = 1 \ldots Y = C Totals
X = 1 O_{11} \ldots O_{1C} O_{1+}
\cdots \cdots \cdots \cdots \cdots
X = R O_{R1} \ldots O_{RC} O_{R+}
Totals O_{+1} \ldots O_{+C} m

  • Hence, testing for independece means testing following hypothesis: \begin{align*} & H_0 \colon X \, \text{ and } \, Y \, \text{ are independent } \\ & H_1 \colon X \, \text{ and } \, Y \, \text{ are not independent } \end{align*}

  • We need to quantify H_0 and H_1

Testing for independence

Y = 1 \ldots Y = C Totals
X = 1 p_{11} \ldots p_{1C} p_{1+}
\cdots \cdots \cdots \cdots \cdots
X = R p_{R1} \ldots p_{RC} p_{R+}
Totals p_{+1} \ldots p_{+C} 1

  • R.v. X and Y are independent iff cell probabilities factor into marginals p_{ij} = P(X = i , Y = j) = P(X = i) P (Y = j) = p_{i+}p_{+j}

  • Therefore the hypothesis test for independence becomes \begin{align*} & H_0 \colon p_{ij} = p_{i+}p_{+j} \quad \text{ for all } \, i = 1, \ldots , R \, \text{ and } \, j = 1 ,\ldots C \\ & H_1 \colon p_{ij} \neq p_{i+}p_{+j} \quad \text{ for some } \, (i,j) \end{align*}

Expected counts

  • Assume the null hypothesis is true H_0 \colon p_{ij} = p_{i+}p_{+j} \quad \text{ for all } \, i = 1, \ldots , R \, \text{ and } \, j = 1 ,\ldots C

  • Under H_0, the expected counts become E_{ij} = m p_{ij} = p_{i+}p_{+j}

  • We need a way to estimate the marginal probabilities p_{i+} and p_{+j}

Estimating marginal probabilities

  • Goal: Estimate marginal probabilities p_{i+} and p_{+j}

  • By definition we have p_{i+} = P( X = i )

  • Hence p_{i+} is probability of and observation to be classified in i-th row

  • Estimate p_{i+} with the proportion of observations classified in i-th row p_{i+} := \frac{o_{i+}}{m} = \frac{ \text{Number of observations in } \, i\text{-th row} }{ \text{ Total number of observations} }

Estimating marginal probabilities

  • Goal: Estimate marginal probabilities p_{i+} and p_{+j}

  • Similarly, by definition p_{+j} = P( Y = j )

  • Hence p_{+j} is probability of and observation to be classified in j-th column

  • Estimate p_{+j} with the proportion of observations classified in j-th column p_{+j} := \frac{o_{+j}}{m} = \frac{ \text{Number of observations in } \, j\text{-th column} }{ \text{ Total number of observations} }

\chi^2 statistic for testing independence

  • Summary: The marginal probabilities are estimated with p_{i+} := \frac{o_{i+}}{m} \qquad \qquad p_{+j} := \frac{o_{+j}}{m}

  • Therefore the expected counts become E_{ij} = m p_{ij} = m p_{i+} p_{+j} = m \left( \frac{o_{i+}}{m} \right) \left( \frac{o_{+j}}{m} \right) = \frac{o_{i+} \, o_{+j}}{m}

  • By the Theorem in Slide 20, the chi-squared statistics satisfies \chi^2 = \sum_{i=1}^R \sum_{j=1}^C \frac{ (O_{ij} - E_{ij})^2 }{ E_{ij} } \ \approx \ \chi^2_{RC - 1 - {\rm fitted}}

  • We need to compute the number of fitted parameters

  • We estimate the first R-1 row marginals by p_{i+} := \frac{o_{i+}}{m} \,, \qquad i = 1 , \ldots, R - 1

  • Since the marginals p_{i+} sum to 1, we can obtain p_{R+} by p_{R+} = 1 - p_{1+} - \ldots - p_{(R-1)+} = 1 - \frac{o_{1+}}{m} - \ldots - \frac{o_{(R-1)+}}{m}

  • Similarly, we estimate the first C-1 column marginals by p_{+j} = \frac{o_{+j}}{m} \,, \qquad j = 1, \ldots, C - 1

  • Since the marginals p_{+j} sum to 1, we can obtain p_{+C} by p_{+C} = 1 - p_{+1} - \ldots - p_{+(C-1)} = 1 - \frac{o_{+1}}{m} - \ldots - \frac{o_{+(C-1)}}{m}

  • In total, we only have to estimate (R - 1) + (C - 1 ) = R + C - 2 parameters

  • Therefore, the fitted parameters are {\rm fitted} = R + C - 2

  • Consequently, the degrees of freedom are \begin{align*} RC - 1 - {\rm fitted} & = RC - 1 - R - C + 2 \\ & = RC - R - C + 1 \\ & = (R - 1)(C - 1) \end{align*}

\chi^2 statistic for testing independence

Conclusion

  • Assume the null hypothesis of row and column independence H_0 \colon p_{ij} = p_{i+}p_{+j} \quad \text{ for all } \, i = 1, \ldots , R \, \text{ and } \, j = 1 ,\ldots C

  • Suppose the counts are O \sim \mathop{\mathrm{Mult}}(m,p), and expected counts are E_{ij} = \frac{o_{i+} \, o_{+j}}{m}

  • By the previous slides, and Theorem in Slide 20 we have that \chi^2 = \sum_{i=1}^R \sum_{j=1}^C \frac{ (O_{ij} - E_{ij})^2 }{ E_{ij} } \approx \ \chi_{RC - 1 - {\rm fitted} }^2 = \chi_{(R-1)(C-1)}^2

\chi^2 statistic for testing independence

Quality of approximation

The chi-squared approximation \chi^2 = \sum_{i=1}^R \sum_{j=1}^C \frac{ (O_{ij} - E_{ij})^2 }{ E_{ij} } \approx \ \chi_{(R-1)(C-1)}^2 is good if E_{ij} \geq 5 \quad \text{ for all } \,\, i = 1 , \ldots , R \, \text{ and } j = 1, \ldots, C

The chi-squared test of independence

Sample:

  • We draw m individuals from population

  • Each individual can be of type (i,j), where

    • i = 1 , \ldots ,R
    • j = 1 , \ldots ,C
    • Total of n = RC types

  • O_{ij} denotes the number of items of type (i,j) drawn

  • p_{ij} is probability of observing type (i,j)

  • p = (p_{ij})_{ij} is probability matrix

  • The matrix of counts O = (o_{ij})_{ij} has multinomial distribution \mathop{\mathrm{Mult}}(m,p)

Data: Matrix of counts, represented by two-way contigency table

Y = 1 \ldots Y = C Totals
X = 1 o_{11} \ldots o_{1C} o_{1+}
\cdots \cdots \cdots \cdots \cdots
X = R o_{R1} \ldots o_{RC} o_{R+}
Totals o_{+1} \ldots o_{+C} m

Hypothesis test: We test for independence of rows and columns \begin{align*} & H_0 \colon X \, \text{ and } \, Y \, \text{ are independent } \\ & H_1 \colon X \, \text{ and } \, Y \, \text{ are not independent } \end{align*}

Procedure: 3 Steps

  1. Calculation:

    • Compute marginal and total counts o_{i+} := \sum_{j=1}^C o_{ij} \,, \qquad o_{+j} := \sum_{i=1}^R o_{ij} \,, \qquad m = \sum_{i=1}^R o_{i+} = \sum_{j=1}^C o_{+j}

    • Compute the expected counts E_{ij} = \frac{o_{i+} \, o_{+j} }{ m }

    • Compute the chi-squared statistic \chi^2 = \sum_{i=1}^R \sum_{j=1}^C \frac{ (o_{ij} - E_{ij})^2 }{E_{ij}}

  1. Statistical Tables or R:
    • Check that E_{ij} \geq 5 for all i and j
    • We fitted R + C - 2 parameters. By the Theorem we get \chi^2 \ \approx \ \chi_{\rm df}^2 \,, \qquad {\rm df} = {\rm degrees \,\, freedom} = (R-1)(C-1)
    • Find critical value \chi^2_{\rm df} (0.05) in chi-squared Table 2
    • Alternatively, compute p-value in R
  2. Interpretation: Reject H_0 when either p < 0.05 \qquad \text{ or } \qquad \chi^2 \in \,\,\text{Rejection Region}
Alternative Rejection Region p-value
X and Y not independent \chi^2 > \chi^2_{\rm{df}}(0.05) P(\chi_{\rm df}^2 > \chi^2)

The chi-squared test of independence in R

  1. Store each row of counts (o_{i1}, o_{i2}, \ldots, o_{iC}) in R vector
    • row_i <- c(o_i1, o_i2, ..., o_iC)
  2. The matrix of counts o = (o_{ij})_{ij} is obtained by assembling rows into a matrix
    • counts <- rbind(row_1, ..., row_R)
  3. Perform a chi-squared goodness-of-fit test on counts with null.p
Alternative R command
X and Y are independent chisq.test(counts)
  1. Read output: In particular look for the p-value

Note: Compute Monte Carlo p-value with option simulate.p.value = TRUE

Part 2:
Worked Example

Example: Residential Status and Region

Owned Rented Total
North West 2180 871 3051
London 1820 1400 3220
South West 1703 614 2317
Total 5703 2885 8588

  • People are sampled at random in NW, London and SW

  • To each person we associate two categories:

    • Residential Status: Rental or Owned
    • Region in which they live: NW, London, SW

  • Question: Are Residential Status and Region independent?

Chi-squared test of independence by hand

  1. Calculation:
    • Total and marginal counts are already provided in the table
Owned Rented Tot
NW 2180 871 o_{1+} = 3051
Lon 1820 1400 o_{2+} = 3220
SW 1703 614 o_{2+} = 2317
Tot o_{+1} = 5703 o_{+2} = 2885 m = 8588

  • Compute the estimated expected counts E_{ij} = \dfrac{o_{i+} \, o_{+j} }{ m }
Owned Rented Tot
NW \frac{3051{\times}5703}{8588} \approx 2026 \frac{3051{\times}2885}{8588} \approx 1025 o_{1+} = 3051
Lon \frac{3220{\times}5703}{8588} \approx 2138 \frac{3220{\times}2885}{8588} \approx 1082 o_{2+} = 3220
SW \frac{2317{\times}5703}{8588} \approx 1539 \frac{2317{\times}1885}{8588} \approx 778 o_{2+} = 2317
Tot o_{+1} = 5703 o_{+2} = 2885 m = 8588

  • Compute the chi-squared statistic \begin{align*} \chi^2 & = \sum_{i=1}^R \sum_{j=1}^C \frac{ (o_{ij} - E_{ij})^2 }{E_{ij}} \\ & = \frac{(2180-2026.066)^2}{2026.066} + \frac{(871-1024.934)^2}{1024.934} \\ & \, + \frac{(1820-2138.293)^2}{2138.293}+\frac{(1400-1081.707)^2}{1081.707} \\ & \, + \frac{(1703-1538.641)^2}{1538.641}+\frac{(614-778.359)^2}{778.359} \\ & = 11.695+23.119 \\ & \, + 47.379+93.658 \\ & \, + 17.557+34.707 \\ & = 228.12 \qquad (2\ \text{d.p.}) \end{align*}

  1. Statistical Tables:
    • Rows are R = 3 and columns are C = 2
    • Degrees of freedom are \, {\rm df} = (R - 1)(C - 1) = 2
    • We clearly have E_{ij} \geq 5 for all i and j
    • Therefore, the following approximation holds \chi^2 \ \approx \ \chi_{(R - 1)(C - 1)}^2 = \chi_{2}^2
    • In chi-squared Table 2, we find critical value \chi^2_{2} (0.05) = 5.99

  1. Interpretation:
    • We have that \chi^2 = 228.12 > 5.99 = \chi_{2}^2 (0.05)
    • Therefore we rejct H_0, meaning that rows and columns are dependent
  • There is evidence (p < 0.05) that Residential Status depends on Region
  • By rescaling table values, we can compute the table of percentages
Owned Rented
North West 71.5\% 28.5\%
London 56.5\% 43.5\%
South West 73.5\% 26.5\%
  • The above suggests that in London fewer homes are Owned and more Rented

Chi-squared test of independence in R

# Store each row into and R vector
row_1 <- c(2180, 871)
row_2 <- c(1820, 1400)
row_3 <- c(1703, 614)

# Assemble the rows into an R matrix
counts <- rbind(row_1, row_2, row_3)

# Perform chi-squared test of independence
ans <- chisq.test(counts)

# Print answer
print(ans)

Output

  • Running the code, we obtain

    Pearson's Chi-squared test

data:  counts
X-squared = 228.11, df = 2, p-value < 2.2e-16


  • This confirms the chi-squared statistic computed by hand \chi^2 = 228.11
  • It also confirms the degrees of freedom \, {\rm df} = 2
  • The p-value is p \approx 0 < 0.05
  • Therefore H_0 is rejected, and Residential Status depends on Region

Exercise: Manchester United performance

Manager Won Drawn Lost
Moyes 27 9 15
Van Gaal 54 25 24
Mourinho 84 32 28
Solskjaer 91 37 40
Rangnick 11 10 8
ten Hag 61 12 28

  • Table contains Man Utd games since 2014 season (updated to 2024)

  • To each Man Utd game in the sample we associate two categories:

    • Manager and Result

  • Question: Is there association between Manager and Team Performance?

Solution

  • To answer the question, we perform chi-squared test of independence in R

  • Test can be performed by suitably modifying the code independence_test.R

# Store each row into and R vector
row_1 <- c(27, 9, 15)
row_2 <- c(54, 25, 24) 
row_3 <- c(84, 32, 28) 
row_4 <- c(91, 37, 40)
row_5 <- c(11, 10, 8)
row_6 <- c(61, 12, 28)

# Assemble the rows into an R matrix
counts <- rbind(row_1, row_2, row_3, row_4, row_5, row_6)

# Perform chi-squared test of independence
ans <- chisq.test(counts)

# Print answer
print(ans)

Output

  • Running the code we obtain

    Pearson's Chi-squared test

data:  counts
X-squared = 12.678, df = 10, p-value = 0.2422


  • p-value is p \approx 0.24 > 0.05
  • We do not reject H_0
  • There is no evidence of association between Manager and Team Performance
  • This suggests that changing the manager alone will not resolve poor performance

Part 3:
Lists

Lists

  • Vectors can contain only one data type (number, character, boolean)

  • Lists are data structures that can contain any R object

  • Lists can be created similarly to vectors, with the command list()

# List containing a number, a vector, and a string
my_list <- list(2, c(T,F,T,T), "hello")

# Print the list
print(my_list)
[[1]]
[1] 2

[[2]]
[1]  TRUE FALSE  TRUE  TRUE

[[3]]
[1] "hello"

Retrieving elements

Elements of a list can be retrieved by indexing

  • my_list[[k]] returns k-th element of my_list


# Consider again the same list
my_list <- list(2, c(T,F,T,T), "hello")

# Access 2nd element of my_list and store it in variable
second_element <- my_list[[2]]

# In this case the variable second_element is a vector
print(second_element)
[1]  TRUE FALSE  TRUE  TRUE

List slicing

You can return multiple items of a list via slicing

  • my_list[c(k1, ..., kn)] returns elements in positions k1, ..., kn
  • my_list[k1:k2] returns elements k1 to k2
my_list <- list(2, c(T,F), "Cat", "Dog", pi, 42)

# We store 1st, 3rd, 5th entries of my_list in slice
slice <- my_list[c(1, 3, 5)]

print(slice)
[[1]]
[1] 2

[[2]]
[1] "Cat"

[[3]]
[1] 3.141593

List slicing

my_list <- list(2, c(T,F), "Cat", "Dog", pi, 42)

# We store 2nd to 4th entries of my_list in slice
slice <- my_list[2:4]

print(slice)
[[1]]
[1]  TRUE FALSE

[[2]]
[1] "Cat"

[[3]]
[1] "Dog"

Naming

  • Components of lists can be named
    • names(my_list) <- c("name_1", ..., "name_k")
# Create list with 3 elements
my_list <- list(2, c(T,F,T,T), "hello")

# Name each of the 3 elements
names(my_list) <- c("number", "TF_vector", "string")

# Print the named list: the list is printed along with element names 
print(my_list)
$number
[1] 2

$TF_vector
[1]  TRUE FALSE  TRUE  TRUE

$string
[1] "hello"

Accessing named entries

  • A component of my_list named my_name can be accessed with dollar operator
    • my_list$my_name
# Create list with 3 elements and name them
my_list <- list(2, c(T,F,T,T), "hello")
names(my_list) <- c("number", "TF_vector", "string")

# Access 2nd element using dollar operator and store it in variable
second_component <- my_list$TF_vector

# Print 2nd element
print(second_component)
[1]  TRUE FALSE  TRUE  TRUE

Naming vectors

  • Vectors can be named, using the same syntax
    • names(my_vector) <- c("name_1", ..., "name_k")


# Create vector storing RGB levels of purple color
purple <- c(99, 3, 48)
names(purple) <- c("Red", "Green", "Blue")

# Print the vector
print(purple)
  Red Green  Blue 
   99     3    48

Accessing named entries

  • A named component is accessed via indexing
    • my_vector["name_k"]


# Print 2nd element
print(purple["Green"])
Green 
    3 


# Print only the value stored in "Green"
print(as.numeric(purple["Green"]))
[1] 3

Part 4:
Data Frames

Data Frames

  • Data Frames are the preferred way of presenting a data set in R:

    • Each variable has assigned a collection of recorded observations

  • Data frames can contain any R object

  • Data Frames are similar to Lists, with the difference that:

    • Members of a Data Frame must all be vectors of equal length

  • In simpler terms:

    • Data Frame is a rectangular table of entries

Constructing a Data Frame

  • Data frames are constructed similarly to lists, using

    • data.frame()

  • Important: Elements of data frame must be vectors of the same length

  • Example: We construct the Family Guy data frame. Variables are

    • person – Name of character
    • age – Age of character
    • sex – Sex of character
family <- data.frame(
  person = c("Peter", "Lois", "Meg", "Chris", "Stewie"),
  age = c(42, 40, 17, 14, 1),
  sex = c("M", "F" , "F", "M", "M")
)

Printing a Data Frame

  • R prints data frames like matrices
  • First row contains vector names
  • First column contains row names
  • Data are paired: e.g. Peter is 42 and Male
family <- data.frame(
  person = c("Peter", "Lois", "Meg", "Chris", "Stewie"),
  age = c(42, 40, 17, 14, 1),
  sex = c("M", "F" , "F", "M", "M")
)

print(family)
  person age sex
1  Peter  42   M
2   Lois  40   F
3    Meg  17   F
4  Chris  14   M
5 Stewie   1   M

Accessing single entry

  • Think of a data frame as a matrix

  • You can access element in position (m,n) by using

    • my_data[m, n]

  • Example

    • Peter is in 1st row
    • Names are in 1st column
    • Therefore, Peter’s name is in position (1,1)
data <- family[1, 1]

print(data)
[1] "Peter"

Accessing multiple entries

To access multiple elements on the same row or column, type

  • my_data[c(k1,...,kn), m] \quad or \quad my_data[k1:k2, m]
  • my_data[n, c(k1,...,km)] \quad or \quad my_data[n, k1:k2]

Example: We want to access Stewie’s Sex and Age:

  • Stewie is listed in 5th row
  • Age and Sex are in 2nd and 3rd column
stewie_data <- family[5, 2:3]

print(stewie_data)
  age sex
5   1   M

Accessing rows

  • To access rows k1,...,kn
    • my_data[c(k1,...,kn), ]
  • To access rows k1 to kn
    • my_data[k1:k2, ]


data <- family[c(1,3), ]      # Access 1st and 3rd row - Peter & Meg

print(data)
  person age sex
1  Peter  42   M
3    Meg  17   F

Accessing columns

  • To access columns k1,...,kn
    • my_data[ , c(k1,...,kn)]
  • To access columns k1 to kn
    • my_data[ ,k1:k2]


age.name <- family[, c(2,1)]    # Access 2nd and 1st columns: Age and Name

print(age.name)
  age person
1  42  Peter
2  40   Lois
3  17    Meg
4  14  Chris
5   1 Stewie

The dollar operator

Use dollar operator to access data frame columns

  • Suppose data frame my_data contains a variable called my_variable
    • my_data$my_variable accesses column my_variable
    • my_data$my_variable is a vector

Example: To access age in the family data frame type

ages <- family$age        # Stores ages in a vector

cat("Ages of the Family Guy characters are:", ages)
Ages of the Family Guy characters are: 42 40 17 14 1
cat("Meg's age is", ages[3])
Meg's age is 17

Size of a data frame

Command Output
nrow(my_data) # of rows
ncol(my_data) # of columns
dim(my_data) vector containing # of rows and columns 


family_dim <- dim(family)    # Stores dimensions of family in a vector

cat("The Family Guy data frame has", 
    family_dim[1], 
    "rows and", 
    family_dim[2], 
    "columns")
The Family Guy data frame has 5 rows and 3 columns

Adding Data

Assume given a data frame my_data

  • To add more records (adding to rows rbind)
    • Create single row data frame new_record
    • new_record must match the structure of my_data
    • Add to my_data with my_data <- rbind(my_data, new_record)
  • To add a set of observations for a new variable (adding to columns cbind)
    • Create a vector new_variable
    • new_variable must have as many components as rows in my_data
    • Add to my_data with my_data <- cbind(my_data, new_variable)

Example: Add new record

  • Consider the usual Family Guy data frame family
  • Suppose we want to add data for Brian
  • Create a new record: a single row data frame with columns
    • person, age, sex
new_record <- data.frame(
  person = "Brian",
  age = 7,
  sex = "M"
)

print(new_record)
  person age sex
1  Brian   7   M

Important: Names have to match existing data frame

Example: Add new record

  • Now, we add new_record to family
  • This is done by appending one row to the existing data frame


family <- rbind(family, new_record)

print(family)
  person age sex
1  Peter  42   M
2   Lois  40   F
3    Meg  17   F
4  Chris  14   M
5 Stewie   1   M
6  Brian   7   M

Example: Add new variable

  • We want to add a new variable to the Family Guy data frame family
  • This variable is called funny
  • It records how funny each character is, with levels
    • Low, Med, High
  • Create a vector funny with entries matching each character (including Brian)
funny <- c("High", "High", "Low", "Med", "High", "Med")

print(funny)
[1] "High" "High" "Low"  "Med"  "High" "Med"

Example: Add new variable

  • Add funny to the Family Guy data frame family
  • This is done by appending one column to the existing data frame
family <- cbind(family, funny)

print(family)
  person age sex funny
1  Peter  42   M  High
2   Lois  40   F  High
3    Meg  17   F   Low
4  Chris  14   M   Med
5 Stewie   1   M  High
6  Brian   7   M   Med

Adding a new variable

Alternative way

Instead of using cbind we can use dollar operator:

  • Want to add variable called new_variable
  • Create a vector v containing values for the new variable
  • v must have as many components as rows in my_data
  • Add to my_data with
    • my_data$new_variable <- v

Example

  • We add age expressed in months to the Family Guy data frame family
  • Age in months can be computed by multiplying vector family$age by 12
v <- family$age * 12       # Computes vector of ages in months

family$age.months <- v     # Stores vector as new column in family

print(family)
  person age sex funny age.months
1  Peter  42   M  High        504
2   Lois  40   F  High        480
3    Meg  17   F   Low        204
4  Chris  14   M   Med        168
5 Stewie   1   M  High         12
6  Brian   7   M   Med         84

Logical Record Subsets

  • We saw how to use logical flag vectors to subset vectors

  • We can use logical flag vectors to subset data frames as well

  • Suppose to have data frame my_data containing a variable my_variable

  • Want to subset records in my_data for which my_variable satisfies a condition

  • Use commands

    • flag <- condition(my_data$my_variable)
    • my_data[flag, ]

Example

  • Consider again the Family Guy data frame family
  • We subset Female characters using flag
    • family$sex == "F"
# Create flag vector for female Family Guy characters
flag <- (family$sex == "F")
print(flag)
[1] FALSE  TRUE  TRUE FALSE FALSE FALSE


# Subset data frame "family" and store in data frame "subset"
subset <- family[flag, ]
print(subset)
  person age sex funny age.months
2   Lois  40   F  High        480
3    Meg  17   F   Low        204

Part 5:
Data Entry

Reading data from files

  • R has a many functions for reading characters from stored files

  • We will see how to read Table-Format files

  • Table-Formats are just tables stored in plain-text files

  • Typical file estensions are:

    • .txt for plain-text files
    • .csv for comma-separated values

  • Table-Formats can be read into R with the command

    • read.table()

Table-Formats

4 key features

  1. Header: Used to name columns
    • Header should be first line
    • Header is optional
    • If header present, need to tell R when importing
    • If not, R cannot tell if first line is header or data
  2. Delimiter: Character used to separate entries in each line
    • Delimiter character cannot be used for anything else in the file
    • Default delimiter is whitespace

Table-Formats

4 key features

  1. Missing value: Character string used exclusively to denote a missing value
    • When reading the file, R will turn these entries into NA
  2. Comments:
    • Table files can include comments
    • Comment lines start with \quad #
    • R ignores such comments

Example

  • Table-Format for Family Guy characters can be downloaded here family_guy.txt
  • The text file looks like this

  • Remarks:
    • Header is present
    • Delimiter is whitespace
    • Missing values denoted by *

read.table command

Table-Formats can be read via read.table()

  • Reads .txt or .csv files

  • outputs a data frame

Options of read.table()

  • header = T/F
    • Tells R if a header is present
  • na.strings = "string"
    • Tells R that "string" means NA (missing values)

Reading our first Table-Format file

To read family_guy.txt into R proceed as follows:

  1. Download family_guy.txt and move file to Desktop

  2. Open the R Console and change working directory to Desktop

# In MacOS type
setwd("~/Desktop")

# In Windows type
setwd("C:/Users/YourUsername/Desktop")

  1. Read family_guy.txt into R and store it in data frame family with code
family = read.table(file = "family_guy.txt",
                    header = TRUE,
                    na.strings = "*")
  1. Note that we are telling read.table() that
    • family_guy.txt has a header
    • Missing values are denoted by *
  1. Print data frame family to screen
print(family)
  person age sex funny age.mon
1  Peter  NA   M  High     504
2   Lois  40   F  <NA>     480
3    Meg  17   F   Low     204
4  Chris  14   M   Med     168
5 Stewie   1   M  High      NA
6  Brian  NA   M   Med      NA
  • For comparison this is the .txt file

Example: t-test

Data: Analysis of Consumer Confidence Index for 2008 crisis (seen in Lecture 3)

  • We imported data into R using c()
  • This is ok for small datasets
  • Suppose the CCI data is stored in a .txt file instead

Goal: Perform t-test on CCI difference for mean difference \mu = 0

  • By reading CCI data into R using read.table()
  • By manipulating CCI data using data frames

  • The CCI dataset can be downloaded here 2008_crisis.txt

  • The text file looks like this

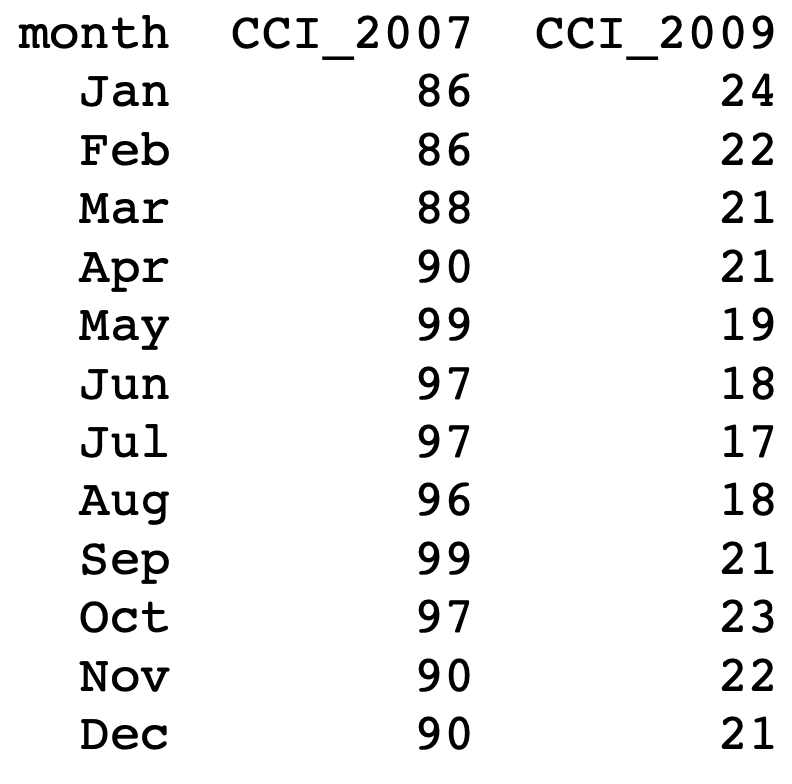
To perform the t-test on data 2008_crisis.txt we proceed as follows:

  1. Download dataset 2008_crisis.txt and move file to Desktop

  2. Open the R Console and change working directory to Desktop

# In MacOS type
setwd("~/Desktop")

# In Windows type
setwd("C:/Users/YourUsername/Desktop")
  1. Read 2008_crisis.txt into R and store it in data frame scores with code
scores = read.table(file = "2008_crisis",
                    header = TRUE
                    )

  1. Store 2nd and 3rd columns of scores into 2 vectors
# CCI from 2007 is stored in 2nd column
score_2007 <- scores[, 2]

# CCI from 2009 is stored in 3nd column
score_2009 <- scores[, 3]
  1. From here, the t-test can be performed as done in Lecture 3
# Compute vector of differences
difference <- score_2007 - score_2009

# Perform t-test on difference with null hypothesis mu = 0
t.test(difference, mu = 0)$p.value
[1] 4.860686e-13
  • We obtain the same result of Lecture 3
    • p-value is p < 0.05 \implies Reject H_0: The mean difference is not 0
  • For convenience, you can download the full code 2008_crisis_code.R

Part 6:
Least squares

Example: Blood Pressure

10 patients treated with both Drug A and Drug B

  • These drugs cause change in blood pressure
  • Patients are given the drugs one at a time
  • Changes in blood pressure are recorded
  • For patient i we denote by
    • x_i the change caused by Drug A
    • y_i the change caused by Drug B
i x_i y_i
1 1.9 0.7
2 0.8 -1.0
3 1.1 -0.2
4 0.1 -1.2
5 -0.1 -0.1
6 4.4 3.4
7 4.6 0.0
8 1.6 0.8
9 5.5 3.7
10 3.4 2.0

Example: Blood Pressure

Goal:

  • Predict reaction to Drug B, knowing reaction to Drug A
  • This means predict y_i from x_i

Plot:

  • To visualize data we can plot pairs (x_i,y_i)
  • Points seem to align
  • It seems there is a linear relation between x_i and y_i

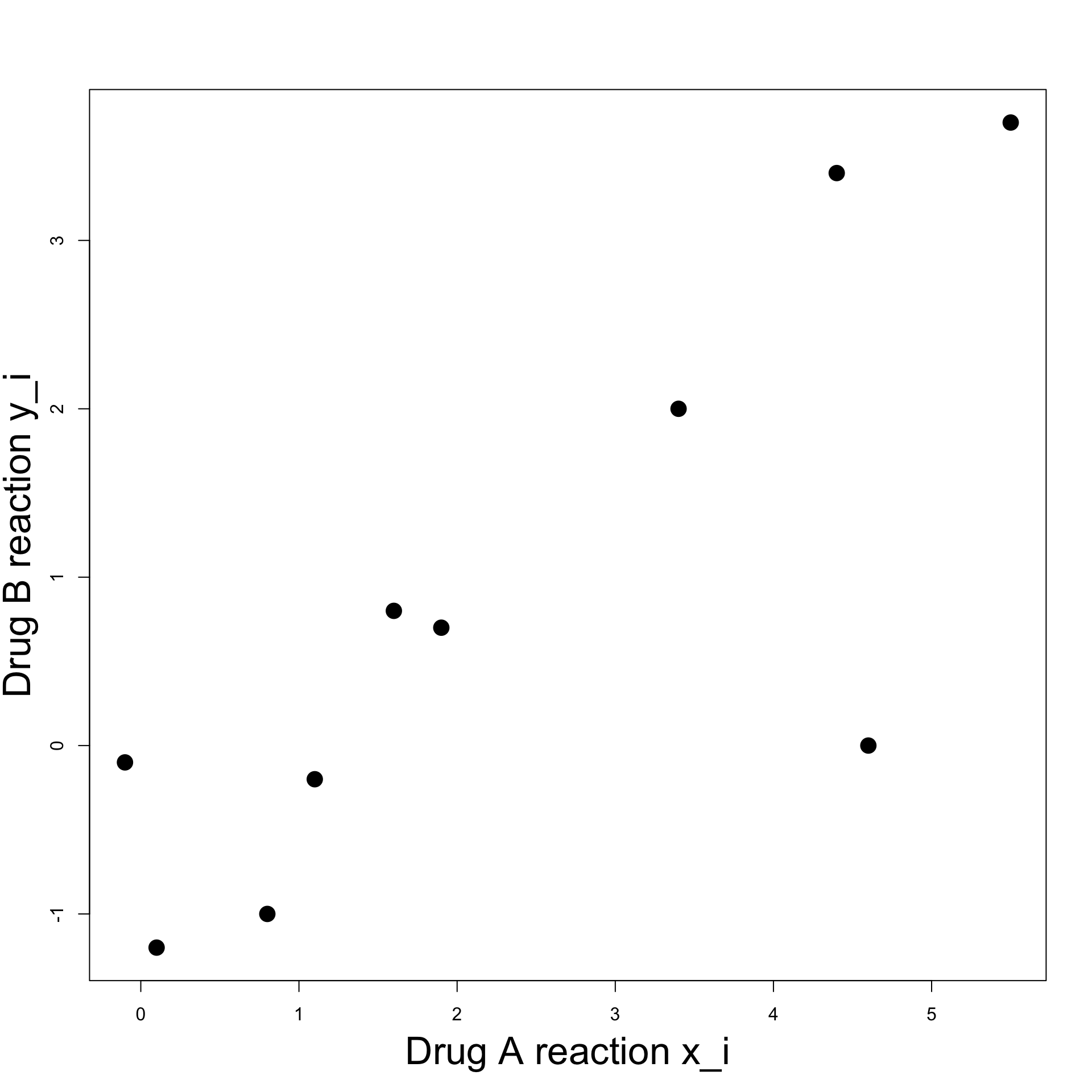
Example: Blood Pressure

Linear relation:

  • Try to fit a line through the data

  • Line roughly predicts y_i from x_i

  • However note the outlier (x_7,y_7) = (4.6, 0) (red point)

  • How is such line constructed?

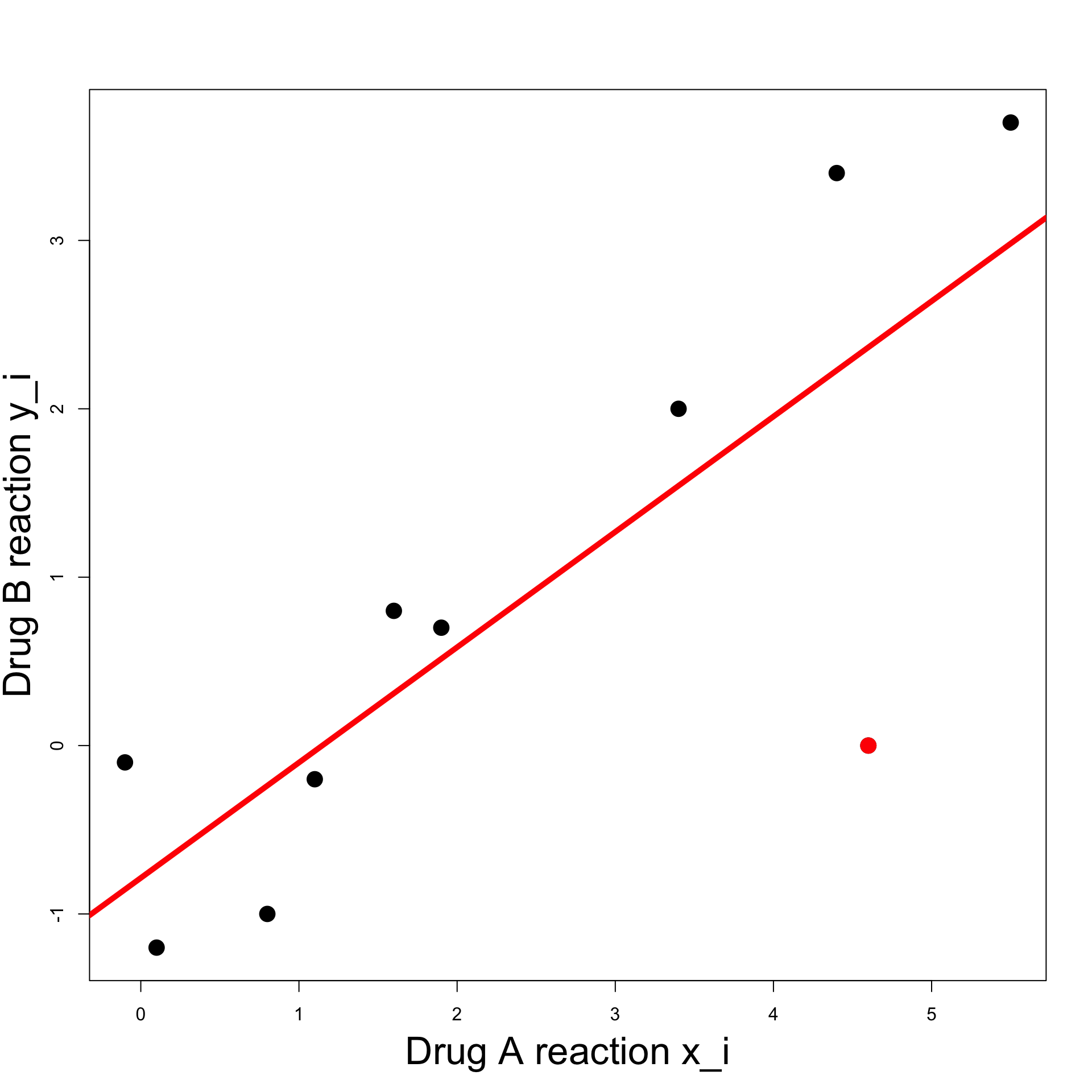
Example: Blood Pressure

Least Squares Line:

  • A general line has equation y = \beta x + \alpha for some
    • slope \beta
    • intercept \alpha
  • Value predicted by the line for x_i is \hat{y}_i = \beta x_i + \alpha

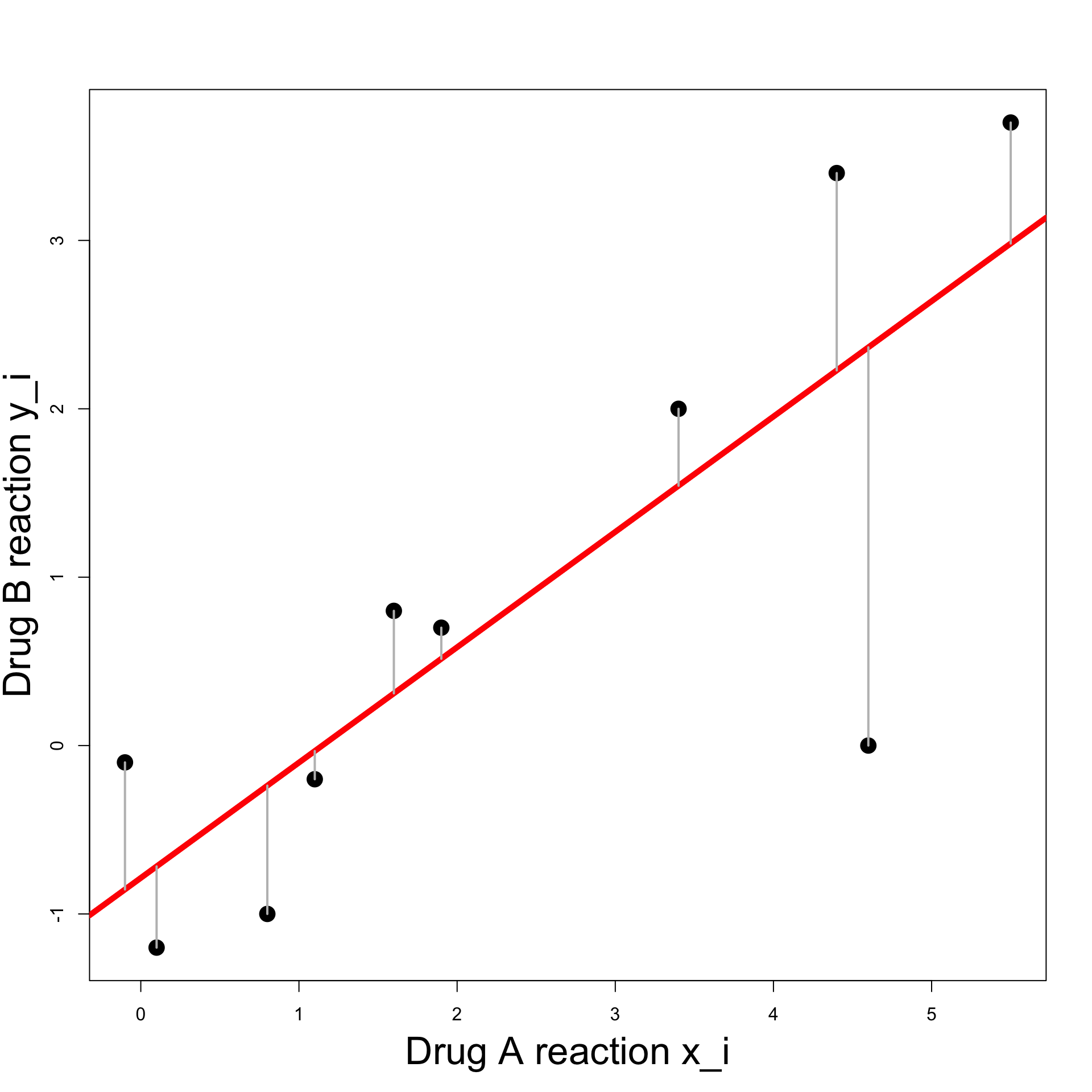
Example: Blood Pressure

Least Squares Line:

  • We would like predicted and actual value to be close \hat{y}_i \approx y_i

  • Hence the vertical difference has to be small y_i - \hat{y}_i \approx 0

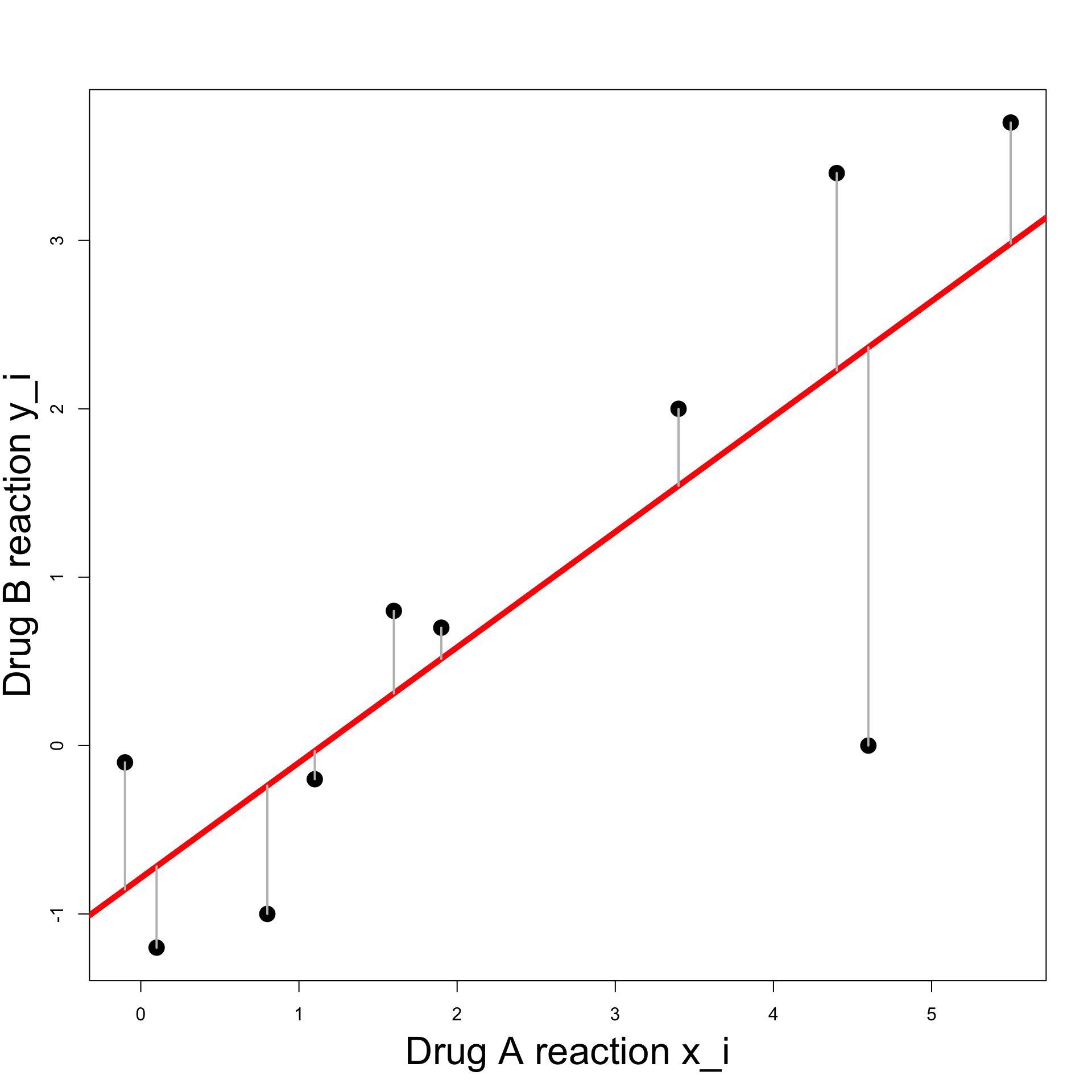
Example: Blood Pressure

Least Squares Line:

  • We want \hat{y}_i - y_i \approx 0 \,, \qquad \forall \, i

  • Can be achieved by minimizing the sum of squares \min_{\alpha, \beta} \ \sum_{i} \ (y_i - \hat{y}_i)^2 \hat{y}_i = \beta x_i + \alpha

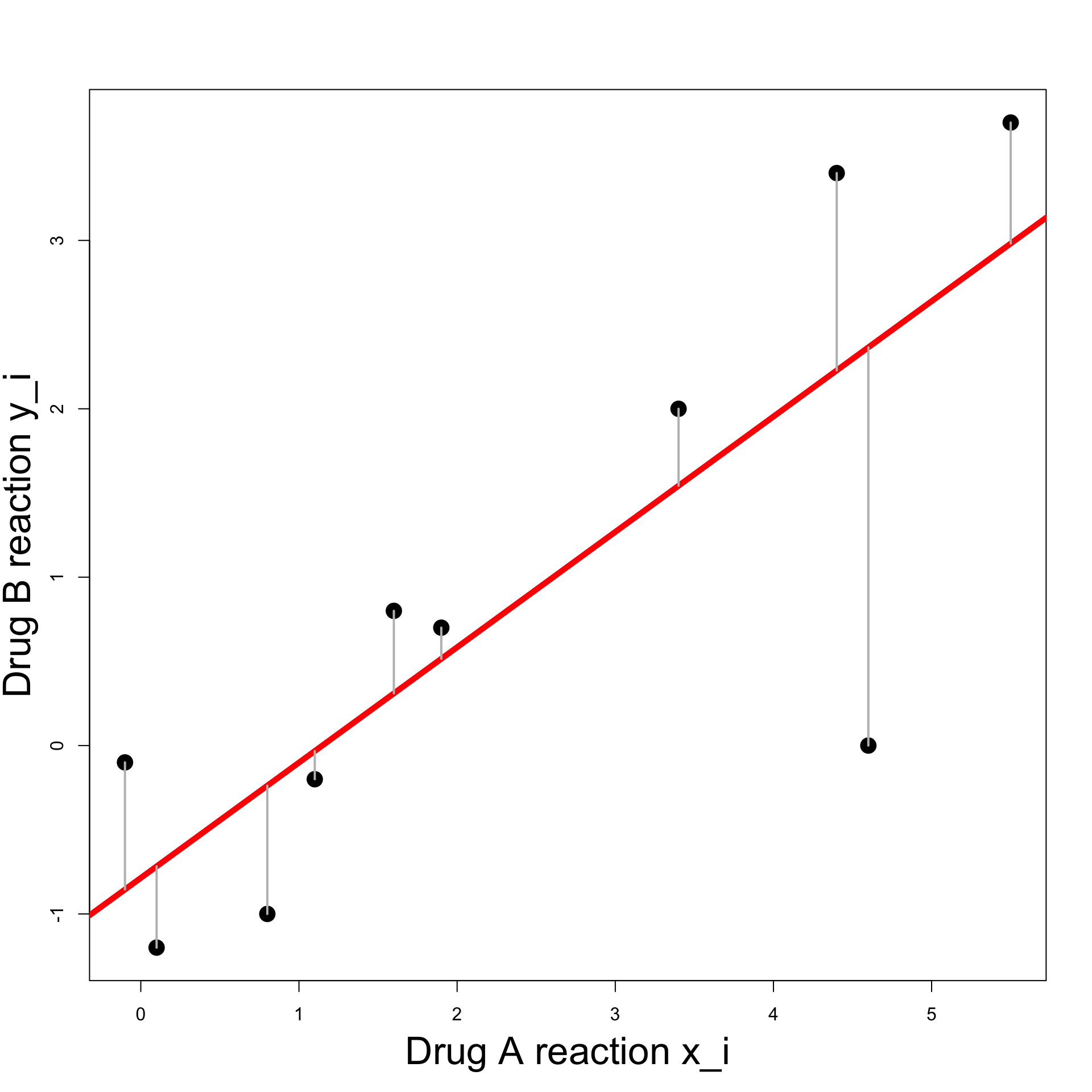
Residual Sum of Squares

Definition
Let (x_1,y_1), \ldots, (x_n, y_n) be a set of n pair of points. Consider the line y = \beta x + \alpha The Residual Sum of Squares associated to the line is \mathop{\mathrm{RSS}}(\alpha,\beta) := \sum_{i=1}^n (y_i-\alpha-{\beta}x_i)^2

Note: \mathop{\mathrm{RSS}} can be seen as a function \mathop{\mathrm{RSS}}\colon \mathbb{R}^2 \to \mathbb{R}\qquad \quad \mathop{\mathrm{RSS}}= \mathop{\mathrm{RSS}}(\alpha,\beta)

\mathop{\mathrm{RSS}}(\alpha,\beta) for Blood Pressure data

Summary statistics

For a given sample (x_1,y_1), \ldots, (x_n, y_n), define

  • Sample Means: \overline{x} := \frac{1}{n} \sum_{i=1}^n x_i \qquad \quad \overline{y} := \frac{1}{n} \sum_{i=1}^n y_i

  • Sums of squares: S_{xx} := \sum_{i=1}^n ( x_i - \overline{x} )^2 \qquad \quad S_{yy} := \sum_{i=1}^n ( y_i - \overline{y} )^2

  • Sum of cross-products: S_{xy} := \sum_{i=1}^n ( x_i - \overline{x} ) ( y_i - \overline{y} )

Minimizing the RSS

Theorem

Given (x_1,y_1), \ldots, (x_n, y_n), consider the minimization problem \begin{equation} \tag{M} \min_{\alpha,\beta } \ \mathop{\mathrm{RSS}}= \min_{\alpha,\beta} \ \sum_{i=1}^n (y_i-\alpha-{\beta}x_i)^2 \end{equation} Then

  1. There exists a unique line solving (M)
  2. Such line has the form y = \hat{\beta} x + \hat{\alpha} with \hat{\beta} = \frac{S_{xy}}{S_{xx}} \qquad \qquad \hat{\alpha} = \overline{y} - \hat{\beta} \ \overline{x}

Positive semi-definite matrix

To prove the Theorem we need some background results

  • A symmetric matrix is positive semi-definite if all the eigenvalues \lambda_i satisfy \lambda_i \geq 0

  • Proposition: A 2 \times 2 symmetric matrix M is positive semi-definite iff \det M \geq 0 \,, \qquad \quad \operatorname{Tr}(M) \geq 0

Positive semi-definite Hessian

  • Suppose given a smooth function of 2 variables

f \colon \mathbb{R}^2 \to \mathbb{R}\qquad \quad f = f (x,y)

  • The Hessian of f is the matrix

\nabla^2 f = \left( \begin{array}{cc} f_{xx} & f_{xy} \\ f_{yx} & f_{yy} \\ \end{array} \right)

Positive semi-definite Hessian

  • In particular the Hessian is positive semi-definite iff

\det \nabla^2 f = f_{xx} f_{yy} - f_{xy}^2 \geq 0 \qquad \quad f_{xx} + f_{yy} \geq 0

  • Side Note: For C^2 functions it holds that

\nabla^2 f \, \text{ is positive semi-definite} \qquad \iff \qquad f \, \text{ is convex}

Optimality conditions

Lemma

Suppose f \colon \mathbb{R}^2 \to \mathbb{R} has positive semi-definite Hessian. They are equivalent

  1. The point (\hat{x},\hat{y}) is a minimizer of f, that is, f(\hat{x}, \hat{y}) = \min_{x,y} \ f(x,y)

  2. The point (\hat{x},\hat{y}) satisfies the optimality conditions \nabla f (\hat{x},\hat{y}) = 0

Note: The proof of the above Lemma can be found in [1]

Example

  • The main example of strictly convex function in 2D is

f(x,y) = x^2 + y^2

  • It is clear that \min_{x,y} \ f(x,y) = \min_{x,y} \ x^2 + y^2 = 0 \,, with the only minimizer being (0,0)

  • However, let us use the Lemma to prove this fact

  • The gradient of f = x^2 + y^2 is

\nabla f = (f_x,f_y) = (2x, 2y)

  • Therefore the optimality condition has unique solution

\nabla f = 0 \qquad \iff \qquad x = y = 0

  • The Hessian of f is

\nabla^2 f = \left( \begin{array}{cc} f_{xx} & f_{xy} \\ f_{yx} & f_{yy} \end{array} \right) = \left( \begin{array}{cc} 2 & 0 \\ 0 & 2 \end{array} \right)

  • The Hessian is positive semi-definite since

\det (\nabla^2) f = 4 > 0 \qquad \qquad \operatorname{Tr}(\nabla^2 f) = 4 > 0

  • By the Lemma, we conclude that (0,0) is the unique minimizer of f, that is,

0 = f(0,0) = \min_{x,y} \ f(x,y)

Minimizing the RSS

Proof of Theorem

  • We go back to proving the RSS Minimization Theorem

  • Suppose given data points (x_1,y_1), \ldots, (x_n, y_n)

  • We want to solve the minimization problem

\begin{equation} \tag{M} \min_{\alpha,\beta } \ \mathop{\mathrm{RSS}}= \min_{\alpha,\beta} \ \sum_{i=1}^n (y_i-\alpha-{\beta}x_i)^2 \end{equation}

  • In order to use the Lemma we need to compute

\nabla \mathop{\mathrm{RSS}}\quad \text{ and } \quad \nabla^2 \mathop{\mathrm{RSS}}

Minimizing the RSS

Proof of Theorem

  • We first compute \nabla \mathop{\mathrm{RSS}} and solve the optimality conditions \nabla \mathop{\mathrm{RSS}}(\alpha,\beta) = 0

  • To this end, recall that \overline{x} := \frac{\sum_{i=1}^nx_i}{n} \qquad \implies \qquad \sum_{i=1}^n x_i = n \overline{x}

  • Similarly, we have \sum_{i=1}^n y_i = n \overline{y}

Minimizing the RSS

Proof of Theorem

  • Therefore we get

\begin{align*} \mathop{\mathrm{RSS}}_{\alpha} & = -2\sum_{i=1}^n(y_i- \alpha- \beta x_i) \\[10pt] & = - 2 n \overline{y} + 2n \alpha + 2 \beta n \overline{x} \\[20pt] \mathop{\mathrm{RSS}}_{\beta} & = -2\sum_{i=1}^n x_i (y_i- \alpha - \beta x_i) \\[10pt] & = - 2 \sum_{i=1}^n x_i y_i + 2 \alpha n \overline{x} + 2 \beta \sum_{i=1}^n x_i^2 \end{align*}

Minimizing the RSS

Proof of Theorem

  • Hence the optimality conditions are

\begin{align} - 2 n \overline{y} + 2n \alpha + 2 \beta n \overline{x} & = 0 \tag{1} \\[20pt] - 2 \sum_{i=1}^n x_i y_i + 2 \alpha n \overline{x} + 2 \beta \sum_{i=1}^n x_i^2 & = 0 \tag{2} \end{align}

Minimizing the RSS

Proof of Theorem

  • Equation (1) is

-2 n \overline{y} + 2n \alpha + 2 \beta n \overline{x} = 0

  • By simplifying and rearraging, we find that (1) is equivalent to

\alpha = \overline{y}- \beta \overline{x}

Minimizing the RSS

Proof of Theorem

  • Equation (2) is equivalent to

\sum_{i=1}^n x_i y_i - \alpha n \overline{x} - \beta \sum_{i=1}^n x^2_i = 0

  • From the previous slide we have \alpha = \overline{y}- \beta \overline{x}

Minimizing the RSS

Proof of Theorem

  • Substituting in Equation (2) we get \begin{align*} 0 & = \sum_{i=1}^n x_i y_i - \alpha n \overline{x} - \beta \sum_{i=1}^n x^2_i \\ & = \sum_{i=1}^n x_i y_i - n \overline{x} \, \overline{y} + \beta n \overline{x}^2 - \beta \sum_{i=1}^n x^2_i \\ & = \sum_{i=1}^n (x_i y_i - \overline{x} \, \overline{y} ) - \beta \left( \sum_{i=1}^n x^2_i - n\overline{x}^2 \right) = S_{xy} - \beta S_{xx} \end{align*} where we used the usual identity S_{xx} = \sum_{i=1}^n ( x_i - \overline{x})^2 = \sum_{i=1}^n x_i^2 - n\overline{x}^2

Minimizing the RSS

Proof of Theorem

  • Hence Equation (2) is equivalent to \beta = \frac{S_{xy}}{ S_{xx} }

  • Also recall that Equation (1) is equivalent to \alpha = \overline{y}- \beta \overline{x}

  • Therefore (\hat\alpha, \hat\beta) solves the optimality conditions \nabla \mathop{\mathrm{RSS}}= 0 iff \hat\alpha = \overline{y}- \hat\beta \overline{x} \,, \qquad \quad \hat\beta = \frac{S_{xy}}{ S_{xx} }

Minimizing the RSS

Proof of Theorem

  • We need to compute \nabla^2 \mathop{\mathrm{RSS}}

  • To this end recall that \mathop{\mathrm{RSS}}_{\alpha} = - 2 n \overline{y} + 2n \alpha + 2 \beta n \overline{x} \,, \quad \mathop{\mathrm{RSS}}_{\beta} = - 2 \sum_{i=1}^n x_i y_i + 2 \alpha n \overline{x} + 2 \beta \sum_{i=1}^n x_i^2

  • Therefore we have \begin{align*} \mathop{\mathrm{RSS}}_{\alpha \alpha} & = 2n \qquad & \mathop{\mathrm{RSS}}_{\alpha \beta} & = 2 n \overline{x} \\ \mathop{\mathrm{RSS}}_{\beta \alpha } & = 2 n \overline{x} \qquad & \mathop{\mathrm{RSS}}_{\beta \beta} & = 2 \sum_{i=1}^{n} x_i^2 \end{align*}

Minimizing the RSS

Proof of Theorem

  • The Hessian determinant is

\begin{align*} \det (\nabla^2 \mathop{\mathrm{RSS}}) & = \mathop{\mathrm{RSS}}_{\alpha \alpha}\mathop{\mathrm{RSS}}_{\beta \beta} - \mathop{\mathrm{RSS}}_{\alpha \beta}^2 \\[10pt] & = 4n \sum_{i=1}^{n} x_i^2 - 4 n^2 \overline{x}^2 \\[10pt] & = 4n \left( \sum_{i=1}^{n} x_i^2 - n \overline{x}^2 \right) \\[10pt] & = 4n S_{xx} \end{align*}

Minimizing the RSS

Proof of Theorem

  • Recall that

S_{xx} = \sum_{i=1}^n (x_i - \overline{x})^2 \geq 0

  • Therefore we have

\det (\nabla^2 \mathop{\mathrm{RSS}}) = 4n S_{xx} \geq 0

Minimizing the RSS

Proof of Theorem

  • We also have

\operatorname{Tr}(\nabla^2\mathop{\mathrm{RSS}}) = \mathop{\mathrm{RSS}}_{\alpha \alpha} + \mathop{\mathrm{RSS}}_{\beta \beta} = 2n + 2 \sum_{i=1}^{n} x_i^2 \geq 0

  • Therefore we have proven \det( \nabla^2 \mathop{\mathrm{RSS}}) \geq 0 \,, \qquad \quad \operatorname{Tr}(\nabla^2\mathop{\mathrm{RSS}}) \geq 0

  • As the Hessian is symmetric, we conclude that \nabla^2 \mathop{\mathrm{RSS}} is positive semi-definite

Minimizing the RSS

Proof of Theorem

  • By the Lemma, we have that all the solutions (\alpha,\beta) to the optimality conditions \nabla \mathop{\mathrm{RSS}}(\alpha,\beta) = 0 are minimizers

  • Therefore (\hat \alpha,\hat\beta) with \hat\alpha = \overline{y}- \hat\beta \overline{x} \,, \qquad \quad \hat\beta = \frac{S_{xy}}{ S_{xx} } is a minimizer of \mathop{\mathrm{RSS}}, ending the proof

Least-squares line

The previous Theorem motivates the following definition

Definition
Given (x_1,y_1), \ldots, (x_n, y_n), the least-squares line is y = \hat\beta x + \hat \alpha where we define \hat{\alpha} = \overline{y} - \hat{\beta} \ \overline{x} \qquad \qquad \hat{\beta} = \frac{S_{xy}}{S_{xx}}

Part 7:
Worked Example

Worked Example: Blood Pressure

Computing the least-squares line in R

In R, we want to do the following:

  • Input the data into vectors x and y

  • Compute the least-square line coefficients \hat{\alpha} = \overline{y} - \hat{\beta} \ \overline{x} \qquad \qquad \hat{\beta} = \frac{S_{xy}}{S_{xx}}

  • Plot the data points (x_i,y_i)

  • Overlay the least squares line

i x_i y_i
1 1.9 0.7
2 0.8 -1.0
3 1.1 -0.2
4 0.1 -1.2
5 -0.1 -0.1
6 4.4 3.4
7 4.6 0.0
8 1.6 0.8
9 5.5 3.7
10 3.4 2.0

First Solution

  • We give a first solution using elementary R functions

  • The code to input the data into a data-frame is as follows

# Input blood pressure changes data into data-frame

changes <- data.frame(drug_A = c(1.9, 0.8, 1.1, 0.1, -0.1, 
                                 4.4, 4.6, 1.6, 5.5, 3.4),
                      drug_B = c(0.7, -1.0, -0.2, -1.2, -0.1, 
                                 3.4, 0.0, 0.8, 3.7, 2.0)
                     )
  • To shorten the code we assign drug_A and drug_B to vectors x and y
# Assign data-frame columns to vectors x and y
x <- changes$drug_A
y <- changes$drug_B

  • Compute averages \overline{x}, \overline{y} and covariances S_{xx}, S_{xy}
# Compute averages xbar and ybar
xbar <- mean(x)
ybar <- mean(y)

# Compute covariances S_xx and S_xy
S_xx <- var(x)
S_xy <- cov(x,y)

  • Compute the least-square line coefficients \hat{\beta} = \frac{S_{xy}}{S_{xx}} \,, \qquad \qquad \hat{\alpha} = \overline{y} - \hat{\beta} \ \overline{x} 
# Compute least-square line coefficients
beta <- S_xy / S_xx
alpha <- ybar - beta * xbar

# Print coefficients
cat("\nCoefficient alpha =", alpha)
cat("\nCoefficient beta =", beta)



Coefficient alpha = -0.7861478

Coefficient beta = 0.685042

  • Plot the data pairs (x_i,y_i)
# Plot the data
plot(x, y, xlab = "", ylab = "", pch = 16, cex = 2)

# Add labels
mtext("Drug A reaction x_i", side = 1, line = 3, cex = 2.1)
mtext("Drug B reaction y_i", side = 2, line = 2.5, cex = 2.1)

Note: We have added a few cosmetic options

  • pch = 16 plots points with black circles
  • cex = 2 stands for character expansion – Specifies width of points
  • mtext is used to fine-tune the axis labels
    • side = 1 stands for x-axis
    • side = 2 stands for y-axis
    • line specifies distance of label from axis

  • To plot a line y = bx + a
    • abline(a, b)
  • Overlay the least squares line y = \hat{\beta}x + \hat{\alpha}
# Overlay least-squares line
abline(a = alpha, b = beta, col = "red", lwd = 3)
  • Note: Cosmetic options
    • col specifies color of the plot
    • lwd specifies line width
  • For clarity, we can add legend to plot
# Add legend
legend("topleft", 
       legend = c("Data", "Least-Squares Line"), 
       col = c("black", "red"), 
       pch = c(16, NA), 
       lty = c(NA, 1), 
       lwd = c(NA, 3))

  • The code can be downloaded here least_squares_1.R

  • Running the code we obtain the plot below

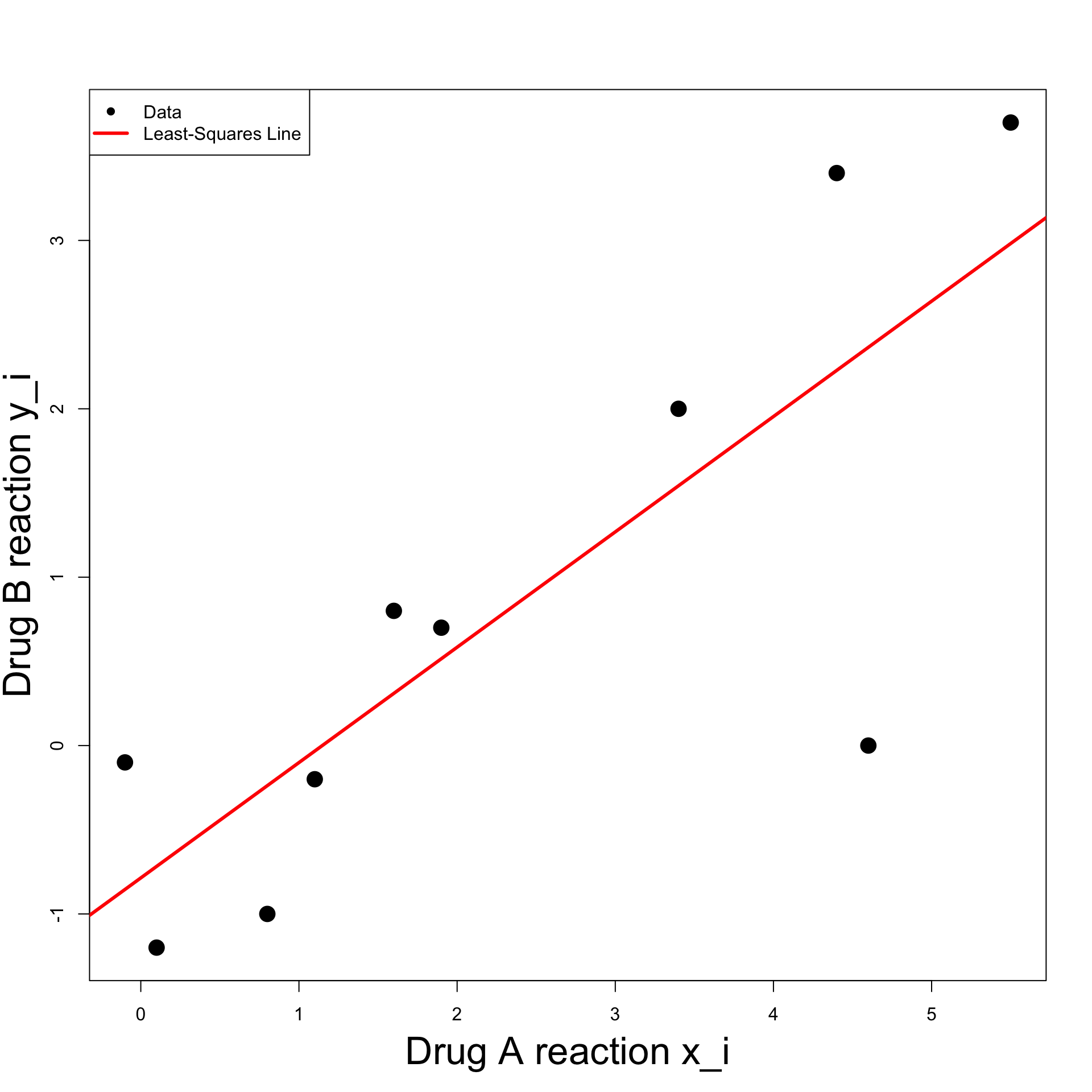
Second Solution

  • The second solution uses the R function lm
  • lm stands for linear model
  • First we input the data into a data-frame
# Input blood pressure changes data into data-frame
changes <- data.frame(drug_A = c(1.9, 0.8, 1.1, 0.1, -0.1, 
                                 4.4, 4.6, 1.6, 5.5, 3.4),
                      drug_B = c(0.7, -1.0, -0.2, -1.2, -0.1, 
                                 3.4, 0.0, 0.8, 3.7, 2.0)
                     )

  • Use lm to fit the least-squares line
    • lm(formula, data)
    • data expects a data-frame in input
    • formula stands for the relation to fit
  • In the case of least-squares:
    • formula = y ~ x
    • x and y are names of two variables in the data-frame
    • Symbol y ~ x can be read as: y modelled as function of x

Note: Storing data in data-frame is optional

  • We can just store data in vectors x and y

  • Then fit the least-squares line with lm(y ~ x)

  • The command to fit the least-squares line on changes is
# Fit least squares line
least_squares <- lm(formula = drug_B ~ drug_A, data = changes) 

# Print output
print(least_squares)

Call:
lm(formula = drug_B ~ drug_A, data = changes)

Coefficients:
(Intercept)       drug_A  
    -0.7861       0.6850


- The above tells us that the estimators are

\hat \alpha = -0.7861 \,, \qquad \quad \hat \beta = 0.6850

  • We can now plot the data with the following command
    • 1st coordinate is the vector changes$drug_A
    • 2nd coordinate is the vector changes$drug_B
# Plot data 
plot(changes$drug_A, changes$drug_B, pch = 16, cex = 2)


  • The least-squares line is currently stored in least_squares

  • To add the line to the current plot use abline

# Plot least-squares line
abline(least_squares, col = "red", lwd = 3)

  • The code can be downloaded here least_squares_2.R

  • Running the code we obtain the plot below

References

Homepage      License      Contact

[1]
Fusco, Nicola, Marcellini, Paolo, Sbordone, Carlo, Mathematical analysis: Functions of several real variables and applications, Springer, 2022.