Statistical Models

Lecture 1

Dr. Silvio Fanzon

S.Fanzon@hull.ac.uk

University of Hull

Lecture 1:
An introduction to Statistics

Outline of Lecture 1

1. Module info
2. Introduction
3. Probability revision I
4. Moment generating functions
5. Probability revision II

Part 1:
Module info

Contact details

• Lecturer: Dr. Silvio Fanzon
• Email: S.Fanzon@hull.ac.uk
• Office: Room 104a, Larkin Building
• Office hours: Thursday 15:00-16:00
• Meetings: in my office or send me an Email

Questions

• If you have any questions please feel free to email me

• We will address Homework and Coursework in class

• In addition, please do not hesitate to attend office hours

Lectures

Each week we have

• 2 Lectures of 2h each
• 1 Tutorial of 1h

Session	Date	Place
Lecture 1	Thu 16:00-18:00	Wilberforce LR 4
Lecture 2	Fri 12:00-14:00	Robert Blackburn LTC
Tutorial	Fri 15:00-16:00	Wilberforce LR 3

Assessment

This module will be assessed as follows:

Type of Assessment	Percentage of final grade
Coursework Portfolio	70%
Homework	30%

Rules for Coursework

• Coursework available on Canvas from Week 9

• Coursework must be submitted on Canvas

• Deadline: 14:00 on Thursday 1st May

• No Late Submission allowed

Rules for Homework

• 10 Homework papers, posted weekly on Canvas

• Each Homework paper is worth 14 points

• Final Homework grade computation:

  • Sum the top 7 scores (max score 98 points)
  • Rescale to 100

• Homework must be submitted on Canvas

• Deadline: 14:00 on Mondays

How to submit assignments

• Submit PDFs only on Canvas

• You have two options:

  • Write on tablet and submit PDF Output
  • Write on paper and Scan in Black and White using a Scanner or Scanner App (Tiny Scanner, Scanner Pro, …)

Important: I will not mark

• Assignments submitted outside of Canvas
• Assignments submitted more than 24h After the Deadline

Key submission dates

Assignment	Due date
Homework 1	3 Feb
Homework 2	10 Feb
Homework 3	17 Feb
Homework 4	24 Feb
Homework 5	3 Mar
Homework 6	10 Mar

Assignment	Due date
Homework 7	17 Mar
Homework 8	24 Mar
Homework 9	31 Mar
Homework 10	7 Apr
Easter 😎	14-25 Apr
Coursework	1 May

References

Main textbooks

Slides are self-contained and based on the book

• [1] Bingham, N. H. and Fry, J. M.
  Regression: Linear models in statistics.
  Springer, 2010

References

Main textbooks

.. and also on the book

• [2] Fry, J. M. and Burke, M.
  Quantitative methods in finance using R.
  Open University Press, 2022

References

Secondary References

• [3] Casella, G. and Berger R. L.
  Statistical inference.
  Second Edition, Brooks/Cole, 2002

• [4] DeGroot M. H. and Schervish M. J.
  Probability and Statistics.
  Fourth Edition, Addison-Wesley, 2012

Probability & Statistics manual

Easier Probability & Statistics manual

References

Secondary References

• [5] Dalgaard, P.
  Introductory statistics with R.
  Second Edition, Springer, 2008

• [6] Davies, T. M.
  The book of R.
  No Starch Press, 2016

Concise Statistics with R

Comprehensive R manual

Part 2:
Introduction

The nature of Statistics

• Statistics is a mathematical subject

• Will use a combination of hand calculation and software (R)

• Software (R) is really useful, particularly for dissertations

• Please bring your laptop into class

• Download R onto your laptop

Overview of the module

Module has 11 Lectures, divided into two parts:

• Part I - Mathematical statistics

• Part II - Applied statistics

Overview of the module

Part I - Mathematical statistics

1. Introduction to statistics
2. Normal distribution family and one-sample hypothesis tests
3. Two-sample hypothesis tests
4. The chi-squared test
5. Non-parametric statistics
6. The maths of regression

Overview of the module

Part II - Applied statistics

7. An introduction to practical regression
8. The extra sum of squares principle and regression modelling assumptions
9. Violations of regression assumptions – Autocorrelation
10. Violation of regression assumptions – Multicollinearity
11. Dummy variable regression models

Simple but useful questions

Generic data:

• What is a typical observation
  • What is the mean?
• How spread out is the data?
  • What is the variance?

Regression:

• What happens to Y as X increases?
  • increases?
  • decreases?
  • nothing?

Statistics answers these questions systematically

• important for large datasets
• The same mathematical machinery (normal family of distributions) can be applied to both questions

Analysing a general dataset

Two basic questions:

1. Location or mean
2. Spread or variance

Statistics enables to answer systematically:

1. One sample and two-sample t-test
2. Chi-squared test and F-test

Recall the following sketch

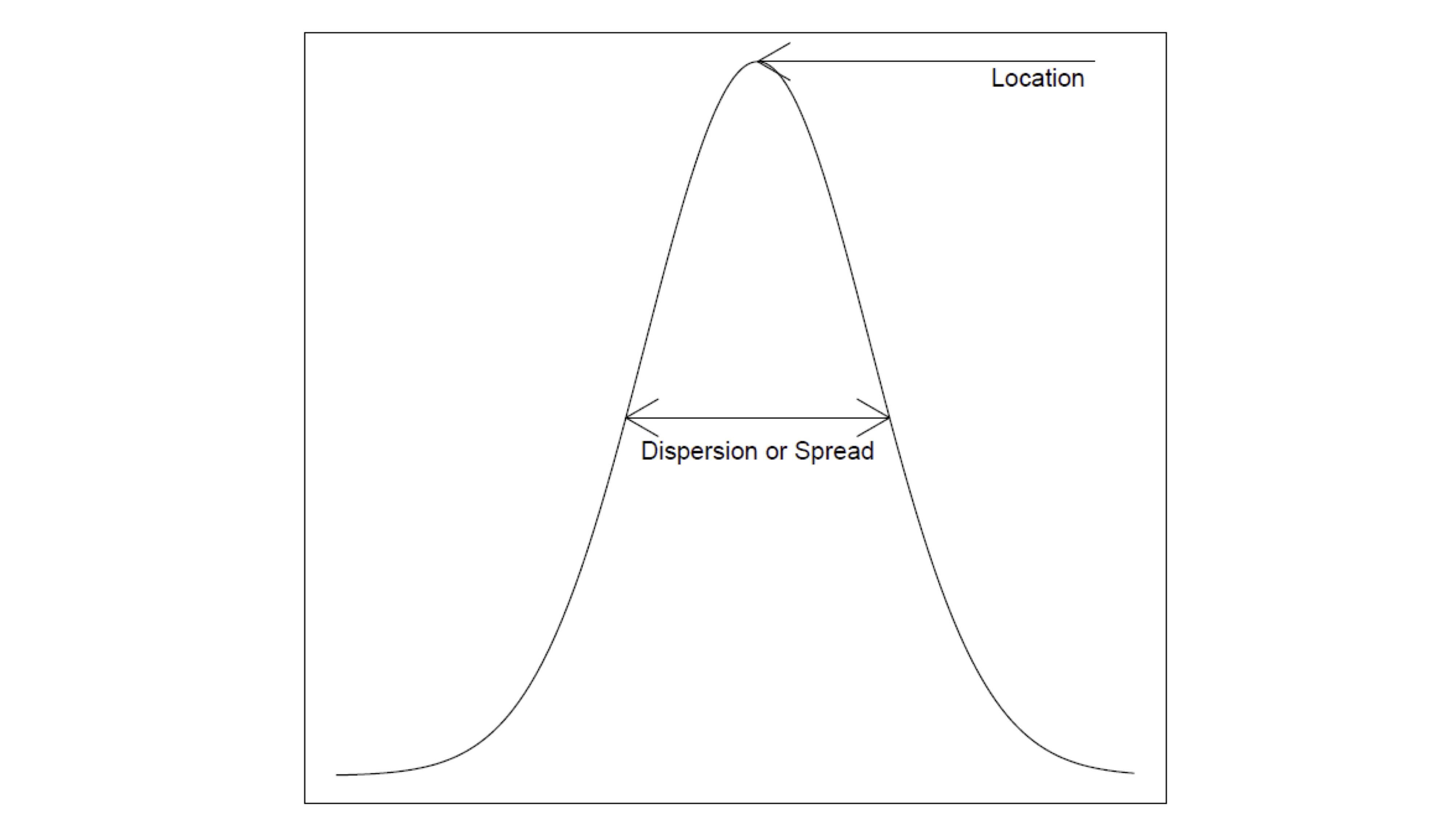
Curve represents data distribution

Motivating regression

Basic question in regression:

• What happens to Y as X increases?

  • increases?
  • decreases?
  • nothing?

In this way regression can be seen as a more advanced version of high-school maths

Positive gradient

As X increases Y increases

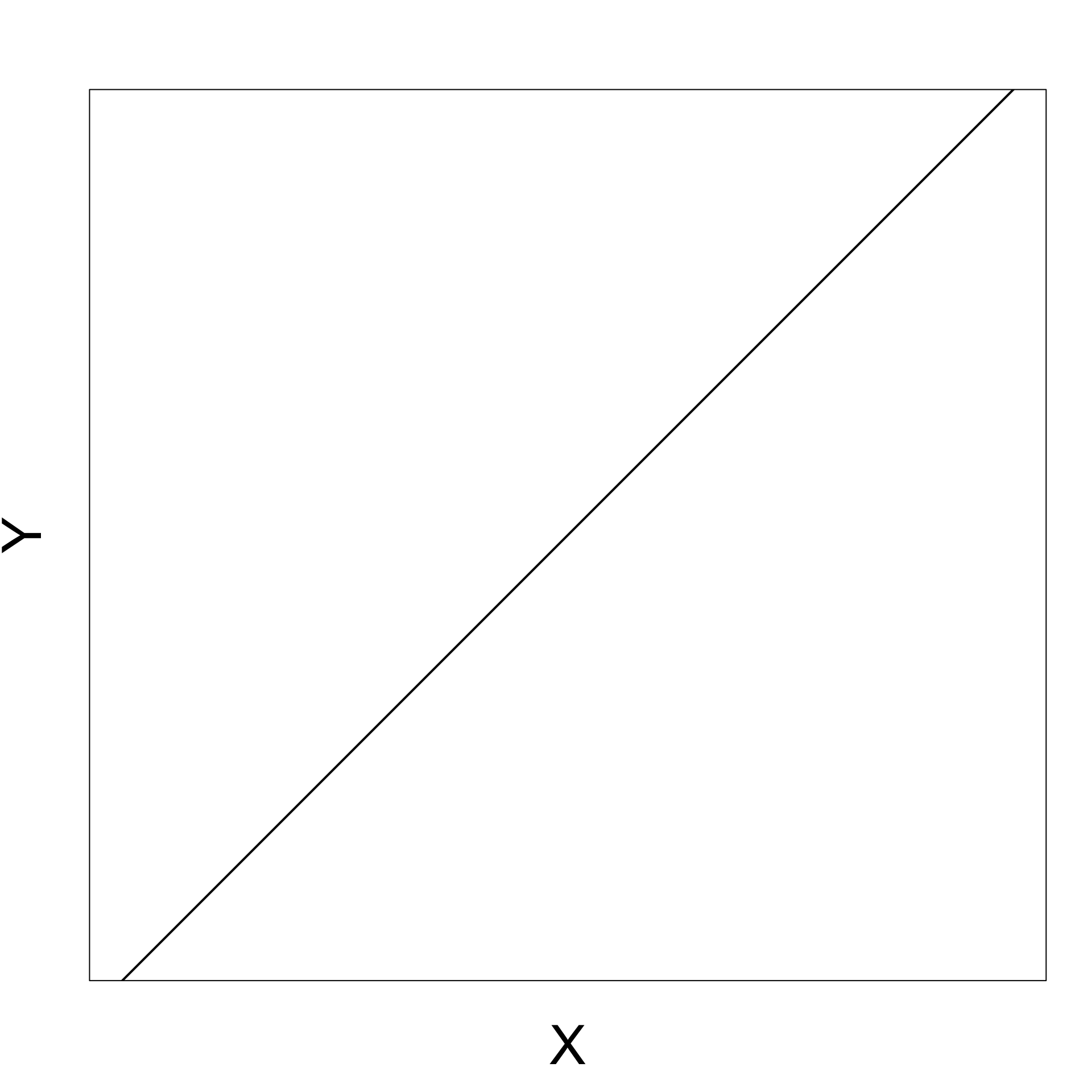
Negative gradient

As X increases Y decreases

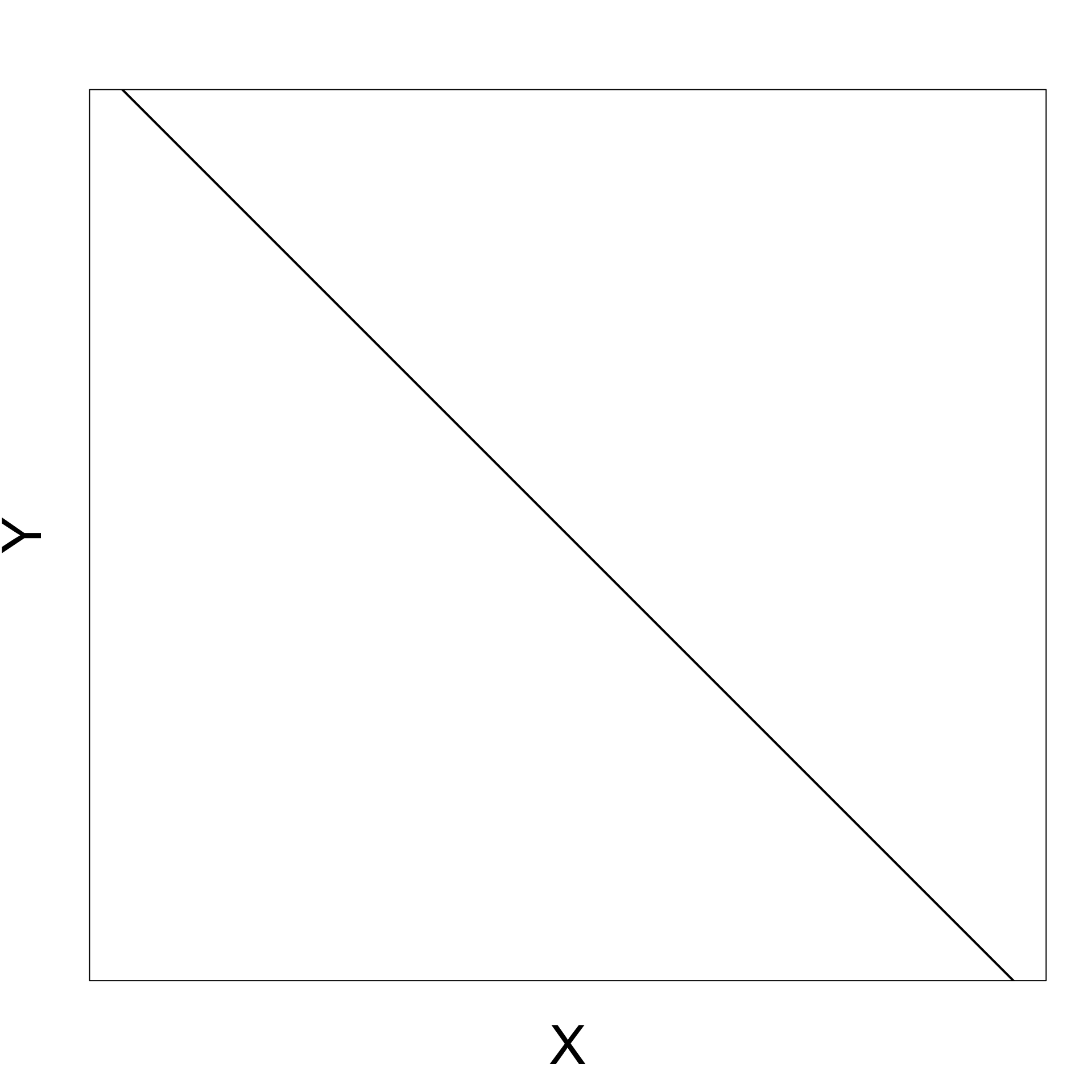
Zero gradient

Changes in X do not affect Y

Real data example

• Real data is more imperfect
• But the same basic idea applies
• Example:
  • X = Stock price
  • Y = Gold price

Real data example

How does real data look like?

Dataset with 33 entries for Stock and Gold price pairs

Stock Price Gold Price 1 3.230426 9.402434 2 2.992937 8.987918 3 2.194025 10.120387 4 2.602475 9.367327 5 2.963497 8.708742 6 4.224242 8.494215 7 7.433981 8.739684 8 5.060836 8.609681 9 3.903316 7.552746 10 4.260542 9.834538 11 3.469490 9.406448

Stock Price Gold Price 12 2.948513 10.62240 13 3.354562 13.12062 14 3.930106 15.05097 15 3.693491 13.39932 16 3.076129 15.34968 17 2.934277 14.83910 18 2.658664 16.01850 19 2.450606 17.25952 20 2.489758 18.26270 21 2.591093 18.13104 22 2.520800 20.20052

Stock Price Gold Price 23 2.471447 24.13767 24 2.062430 30.07695 25 1.805153 35.69485 26 1.673950 39.29658 27 1.620848 39.52317 28 1.547374 36.12564 29 1.721679 31.01106 30 1.974891 29.60810 31 2.168978 35.00593 32 2.277214 37.62929 33 2.993353 41.45828

Real data example

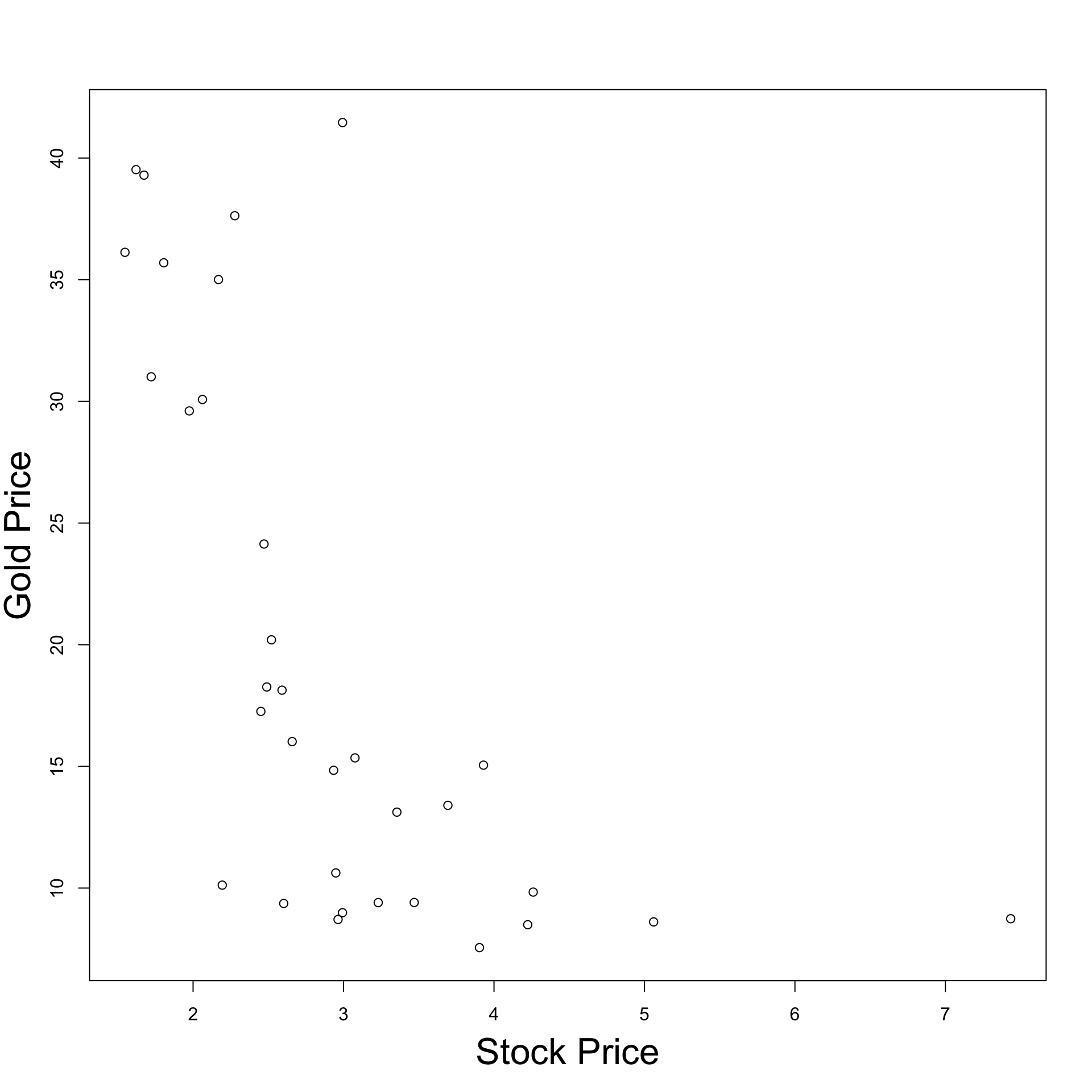
Visualizing the data

• Plot Stock Price against Gold Price

• Observation:

  • As Stock price decreases, Gold price increases

• Why? This might be because:

  • Stock price decreases
  • People invest in secure assets (Gold)
  • Gold demand increases
  • Gold price increases

Part 3:
Probability revision I

Probability revision I

• You are expected to be familiar with the main concepts from Y1 module
  Introduction to Probability & Statistics

• Self-contained revision material available in Appendix A

Topics to review: Sections 1–3 of Appendix A

• Sample space
• Events
• Probability measure
• Conditional probability
• Events independence

• Random Variable (Discrete and Continuous)
• Distribution
• cdf, pmf, pdf
• Expected value and Variance

Summary - Random Variables

• Given probability space (\Omega, \mathcal{B}, P) and a Random Variable X \colon \Omega \to \mathbb{R}

• Cumulative Density Function (cdf): F_X(x) := P(X \leq x)

Discrete RV	Continuous RV
F_X has jumps	F_X is continuous
Probability Mass Function (pmf)	Probability Density Function (pdf)
f_X(x) := P(X=x)	f_X(x) := F_X'(x)
f_X \geq 0	f_X \geq 0
\sum_{x=-\infty}^\infty f_X(x) = 1	\int_{-\infty}^\infty f_X(x) \, dx = 1
F_X (x) = \sum_{k=-\infty}^x f_X(k)	F_X (x) = \int_{-\infty}^x f_X(t) \, dt
P(a \leq X \leq b) = \sum_{k = a}^{b} f_X(k)	P(a \leq X \leq b) = \int_a^b f_X(t) \, dt

Expected Value

• Suppose X \colon \Omega \to \mathbb{R} is RV and g \colon \mathbb{R}\to \mathbb{R} a function
• Then g(X) \colon \Omega \to \mathbb{R} is a RV

Definition

The expected value of the random variable g(X) is

\begin{align*} {\rm I\kern-.3em E}[g(X)] & := \sum_{x} g(x) f_X(x) = \sum_{x \in \mathbb{R}} g(x) P(X = x) \quad \text{ if } X \text{ discrete} \\ {\rm I\kern-.3em E}[g(X)] & := \int_{-\infty}^{\infty} g(x) f_X(x) \, dx \quad \text{ if } X \text{ continuous} \end{align*}

Expected Value

Properties

In particular we have¹

• If X discrete {\rm I\kern-.3em E}[X] = \sum_{x \in \mathbb{R}} x f_X(x) = \sum_{x \in \mathbb{R}} x P(X = x)

• If X continuous {\rm I\kern-.3em E}[X] = \int_{-\infty}^{\infty} x f_X(x) \, dx

1. These follow by taking g(x)=x in previous definitions, so that g(X) = X

Variance

Variance measures how much a rv X deviates from {\rm I\kern-.3em E}[X]

Definition: Variance

The variance of a random variable X is {\rm Var}[X]:= {\rm I\kern-.3em E}[(X - {\rm I\kern-.3em E}[X])^2]

Proposition: Useful formula for variance

{\rm Var}[X] = {\rm I\kern-.3em E}[X^2] - {\rm I\kern-.3em E}[X]^2

Example - Gamma distribution

Definition

The Gamma distribution with parameters \alpha,\beta>0 is f(x) := \frac{x^{\alpha-1} e^{-\beta{x}} \beta^{\alpha}}{\Gamma(\alpha)} \,, \quad x > 0 where \Gamma is the Gamma function \Gamma(a) :=\int_0^{\infty} x^{a-1} e^{-x} \, dx

Example - Gamma distribution

Definition

Properties of \Gamma:

• The Gamma function coincides with the factorial on natural numbers \Gamma(n)=(n-1)! \,, \quad \forall \, n \in \mathbb{N}

• More in general \Gamma(a)=(a-1)\Gamma(a-1) \,, \quad \forall \, a > 0

• Definition of \Gamma implies normalization of the Gamma distribution: \int_0^{\infty} f(x) \,dx = \int_0^{\infty} \frac{x^{\alpha-1} e^{-\beta{x}} \beta^{\alpha}}{\Gamma(\alpha)} \, dx = 1

Example - Gamma distribution

Definition

X has Gamma distribution with parameters \alpha,\beta if

• the pdf of X is f_X(x) = \begin{cases} \dfrac{x^{\alpha-1} e^{-\beta{x}} \beta^{\alpha}}{\Gamma(\alpha)} & \text{ if } x > 0 \\ 0 & \text{ if } x \leq 0 \end{cases}

• In this case we write X \sim \Gamma(\alpha,\beta)

• \alpha is shape parameter

• \beta is rate parameter

Example - Gamma distribution

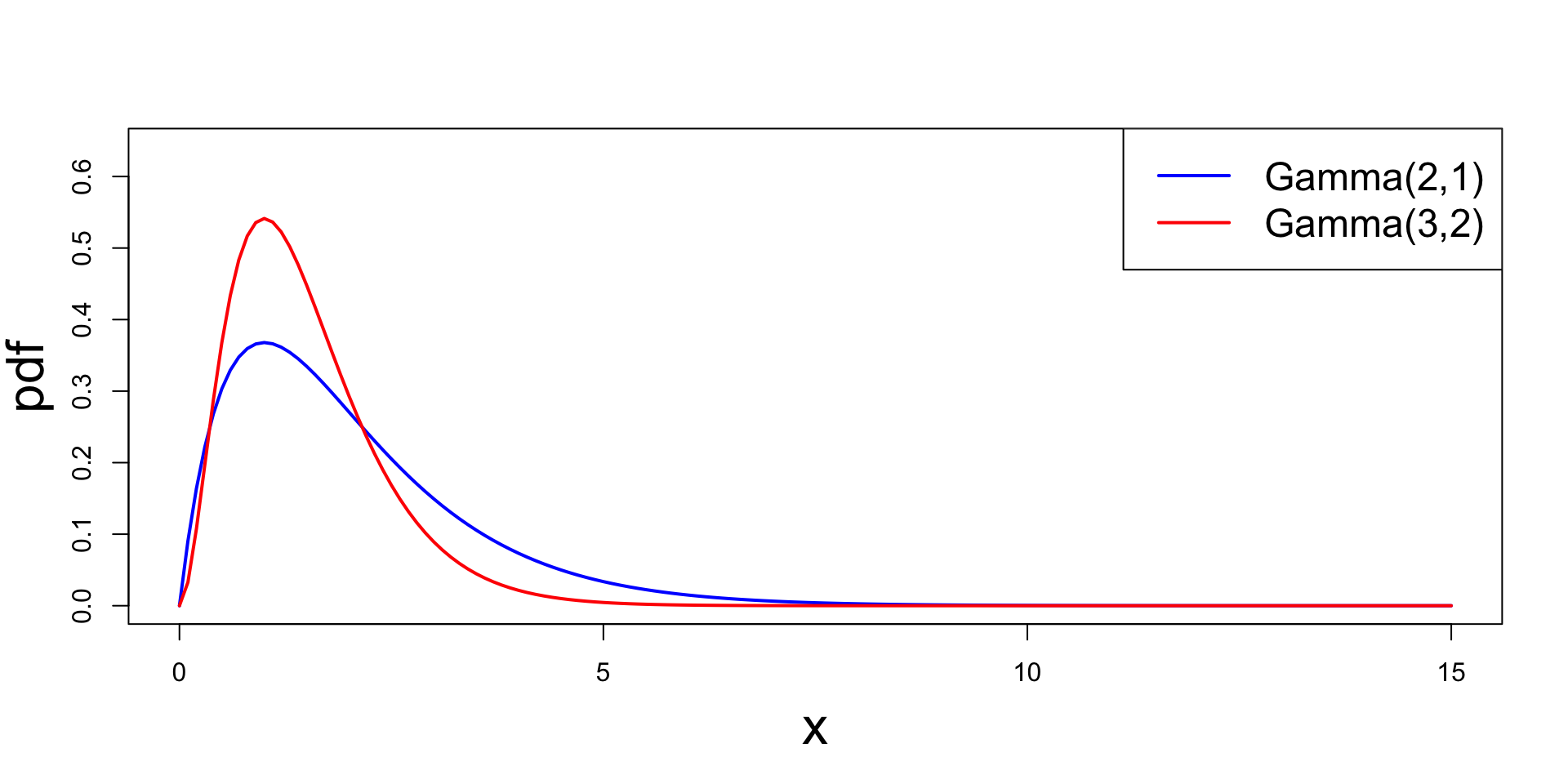
Plot

Plotting \Gamma(\alpha,\beta) for parameters (2,1) and (3,2)

Example - Gamma distribution

Expected value

Let X \sim \Gamma(\alpha,\beta). We have: \begin{align*} {\rm I\kern-.3em E}[X] & = \int_{-\infty}^\infty x f_X(x) \, dx \\ & = \int_0^\infty x \, \frac{x^{\alpha-1} e^{-\beta{x}} \beta^{\alpha}}{\Gamma(\alpha)} \, dx \\ & = \frac{ \beta^{\alpha} }{ \Gamma(\alpha) } \int_0^\infty x^{\alpha} e^{-\beta{x}} \, dx \end{align*}

Example - Gamma distribution

Expected value

Recall previous calculation: {\rm I\kern-.3em E}[X] = \frac{ \beta^{\alpha} }{ \Gamma(\alpha) } \int_0^\infty x^{\alpha} e^{-\beta{x}} \, dx Change variable y=\beta x and recall definition of \Gamma: \begin{align*} \int_0^\infty x^{\alpha} e^{-\beta{x}} \, dx & = \int_0^\infty \frac{1}{\beta^{\alpha}} (\beta x)^{\alpha} e^{-\beta{x}} \frac{1}{\beta} \, \beta \, dx \\ & = \frac{1}{\beta^{\alpha+1}} \int_0^\infty y^{\alpha} e^{-y} \, dy \\ & = \frac{1}{\beta^{\alpha+1}} \Gamma(\alpha+1) \end{align*}

Example - Gamma distribution

Expected value

Therefore \begin{align*} {\rm I\kern-.3em E}[X] & = \frac{ \beta^{\alpha} }{ \Gamma(\alpha) } \int_0^\infty x^{\alpha} e^{-\beta{x}} \, dx \\ & = \frac{ \beta^{\alpha} }{ \Gamma(\alpha) } \, \frac{1}{\beta^{\alpha+1}} \Gamma(\alpha+1) \\ & = \frac{\Gamma(\alpha+1)}{\beta \Gamma(\alpha)} \end{align*}

Recalling that \Gamma(\alpha+1)=\alpha \Gamma(\alpha): {\rm I\kern-.3em E}[X] = \frac{\Gamma(\alpha+1)}{\beta \Gamma(\alpha)} = \frac{\alpha}{\beta}

Example - Gamma distribution

Variance

We want to compute {\rm Var}[X] = {\rm I\kern-.3em E}[X^2] - {\rm I\kern-.3em E}[X]^2

• We already have {\rm I\kern-.3em E}[X]
• Need to compute {\rm I\kern-.3em E}[X^2]

Example - Gamma distribution

Variance

Proceeding similarly we have:

\begin{align*} {\rm I\kern-.3em E}[X^2] & = \int_{-\infty}^{\infty} x^2 f_X(x) \, dx \\ & = \int_{0}^{\infty} x^2 \, \frac{ x^{\alpha-1} \beta^{\alpha} e^{- \beta x} }{ \Gamma(\alpha) } \, dx \\ & = \frac{\beta^{\alpha}}{\Gamma(\alpha)} \int_{0}^{\infty} x^{\alpha+1} e^{- \beta x} \, dx \end{align*}

Example - Gamma distribution

Variance

Recall previous calculation: {\rm I\kern-.3em E}[X^2] = \frac{\beta^{\alpha}}{\Gamma(\alpha)} \int_{0}^{\infty} x^{\alpha+1} e^{- \beta x} \, dx Change variable y=\beta x and recall definition of \Gamma: \begin{align*} \int_0^\infty x^{\alpha+1} e^{-\beta{x}} \, dx & = \int_0^\infty \frac{1}{\beta^{\alpha+1}} (\beta x)^{\alpha + 1} e^{-\beta{x}} \frac{1}{\beta} \, \beta \, dx \\ & = \frac{1}{\beta^{\alpha+2}} \int_0^\infty y^{\alpha + 1 } e^{-y} \, dy \\ & = \frac{1}{\beta^{\alpha+2}} \Gamma(\alpha+2) \end{align*}

Example - Gamma distribution

Variance

Therefore {\rm I\kern-.3em E}[X^2] = \frac{ \beta^{\alpha} }{ \Gamma(\alpha) } \int_0^\infty x^{\alpha+1} e^{-\beta{x}} \, dx = \frac{ \beta^{\alpha} }{ \Gamma(\alpha) } \, \frac{1}{\beta^{\alpha+2}} \Gamma(\alpha+2) = \frac{\Gamma(\alpha+2)}{\beta^2 \Gamma(\alpha)} Now use following formula twice \Gamma(\alpha+1)=\alpha \Gamma(\alpha): \Gamma(\alpha+2)= (\alpha + 1) \Gamma(\alpha + 1) = (\alpha + 1) \alpha \Gamma(\alpha) Substituting we get {\rm I\kern-.3em E}[X^2] = \frac{\Gamma(\alpha+2)}{\beta^2 \Gamma(\alpha)} = \frac{(\alpha+1) \alpha}{\beta^2}

Example - Gamma distribution

Variance

Therefore {\rm I\kern-.3em E}[X] = \frac{\alpha}{\beta} \quad \qquad {\rm I\kern-.3em E}[X^2] = \frac{(\alpha+1) \alpha}{\beta^2} and the variance is \begin{align*} {\rm Var}[X] & = {\rm I\kern-.3em E}[X^2] - {\rm I\kern-.3em E}[X]^2 \\ & = \frac{(\alpha+1) \alpha}{\beta^2} - \frac{\alpha^2}{\beta^2} \\ & = \frac{\alpha}{\beta^2} \end{align*}

Part 4:
Moment generating functions

Moment generating function

• We abbreviate Moment generating function with MGF

• MGF provides a short-cut to calculating mean and variance

Definition

The moment generating function or MGF of a rv X is M_X(t) := {\rm I\kern-.3em E}[e^{tX}] \,, \quad \forall \, t \in \mathbb{R}

In particular we have:

• X discrete: M_X(t) = \sum_{x \in \mathbb{R}} e^{tx} f_X(x)

• X continuous: M_X(t) = \int_{-\infty}^\infty e^{tx} f_X(x) \, dx

Moment generating function

Computing moments

Theorem

If X has MGF M_X then {\rm I\kern-.3em E}[X^n] = M_X^{(n)} (0) where we denote M_X^{(n)} (0) := \frac{d^n}{dt^n} M_X^{(n)}(t) \bigg|_{t=0}

The quantity {\rm I\kern-.3em E}[X^n] is called n-th moment of X

Moment generating function

Proof of Theorem

Suppose X continuous and that we can exchange derivative and integral: \begin{align*} \frac{d}{dt} M_X(t) & = \frac{d}{dt} \int_{-\infty}^\infty e^{tx} f_X(x) \, dx = \int_{-\infty}^\infty \left( \frac{d}{dt} e^{tx} \right) f_X(x) \, dx \\ & = \int_{-\infty}^\infty xe^{tx} f_X(x) \, dx = {\rm I\kern-.3em E}(Xe^{tX}) \end{align*} Evaluating at t = 0: \frac{d}{dt} M_X(t) \bigg|_{t = 0} = {\rm I\kern-.3em E}(Xe^{0}) = {\rm I\kern-.3em E}[X]

Moment generating function

Proof of Theorem

Proceeding by induction we obtain: \frac{d^n}{dt^n} M_X(t) = {\rm I\kern-.3em E}(X^n e^{tX}) Evaluating at t = 0 yields the thesis: \frac{d^n}{dt^n} M_X(t) \bigg|_{t = 0} = {\rm I\kern-.3em E}(X^n e^{0}) = {\rm I\kern-.3em E}[X^n]

Moment generating function

Notation

For the first 3 derivatives we use special notations:

M_X'(0) := M^{(1)}_X(0) = {\rm I\kern-.3em E}[X] M_X''(0) := M^{(2)}_X(0) = {\rm I\kern-.3em E}[X^2] M_X'''(0) := M^{(3)}_X(0) = {\rm I\kern-.3em E}[X^3]

Example - Normal distribution

Definition

• The normal distribution with mean \mu and variance \sigma^2 is f(x) := \frac{1}{\sqrt{2\pi\sigma^2}} \, \exp\left( -\frac{(x-\mu)^2}{2\sigma^2}\right) \,, \quad x \in \mathbb{R}

• X has normal distribution with mean \mu and variance \sigma^2 if f_X = f

  • In this case we write X \sim N(\mu,\sigma^2)

• The standard normal distribution is denoted N(0,1)

Example - Normal distribution

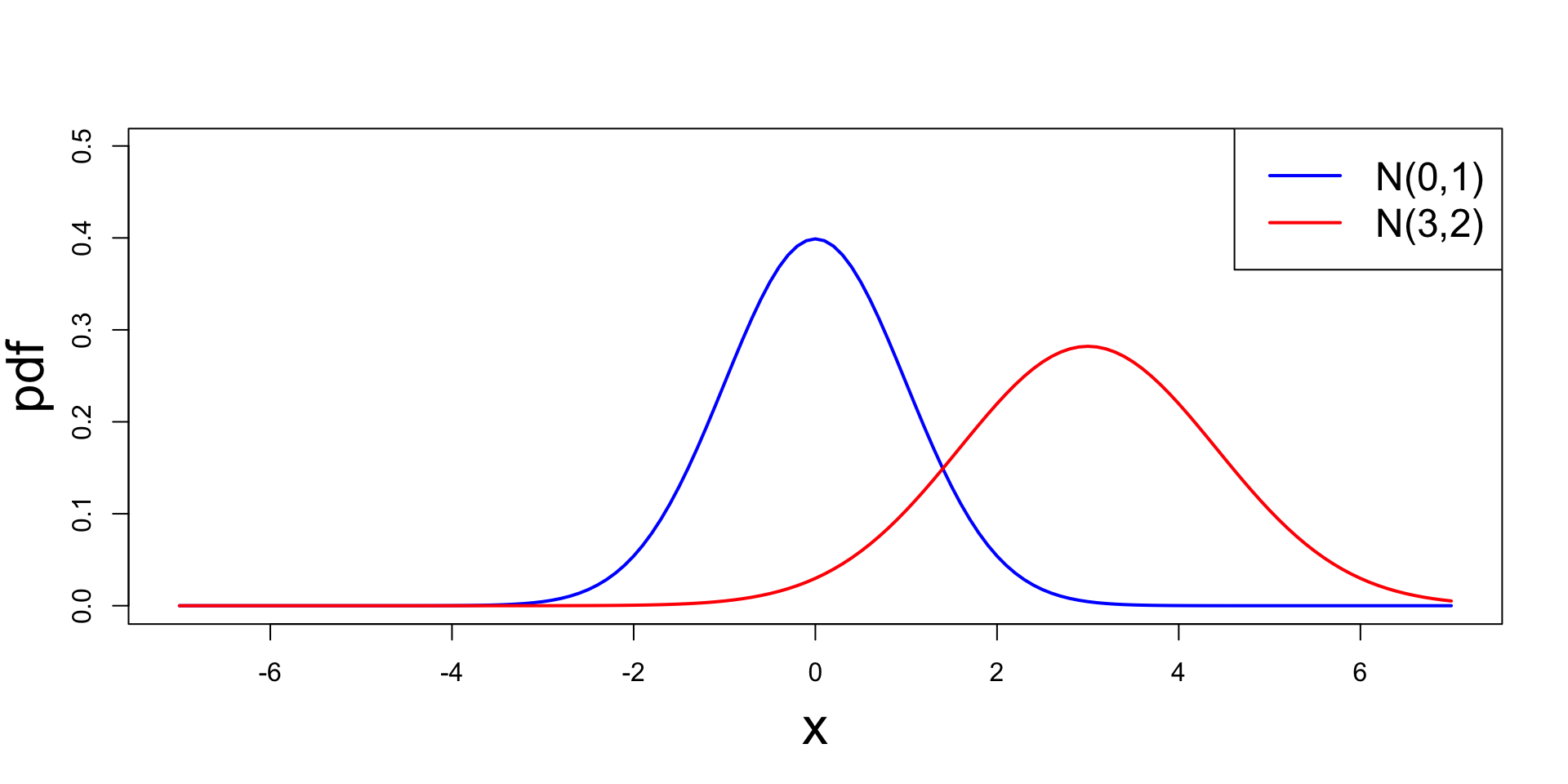
Plot

Plotting N(\mu,\sigma^2) for parameters (0,1) and (3,2)

Example - Normal distribution

Moment generating function

The equation for the normal pdf is f_X(x) = \frac{1}{\sqrt{2\pi\sigma^2}} \, \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right) Being pdf, we must have \int f_X(x) \, dx = 1. This yields: \begin{equation} \tag{1} \int_{-\infty}^{\infty} \exp \left( -\frac{x^2}{2\sigma^2} + \frac{\mu{x}}{\sigma^2} \right) \, dx = \exp \left(\frac{\mu^2}{2\sigma^2} \right) \sqrt{2\pi} \sigma \end{equation}

Example - Normal distribution

Moment generating function

We have \begin{align*} M_X(t) & := {\rm I\kern-.3em E}(e^{tX}) = \int_{-\infty}^{\infty} e^{tx} f_X(x) \, dx \\ & = \int_{-\infty}^{\infty} e^{tx} \frac{1}{\sqrt{2\pi}\sigma} \exp \left( -\frac{(x-\mu)^2}{2\sigma^2} \right) \, dx \\ & = \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{\infty} e^{tx} \exp \left( -\frac{x^2}{2\sigma^2} - \frac{\mu^2}{2\sigma^2} + \frac{x\mu}{\sigma^2} \right) \, dx \\ & = \exp\left(-\frac{\mu^2}{2\sigma^2} \right) \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{\infty} \exp \left(- \frac{x^2}{2\sigma^2} + \frac{(t\sigma^2+\mu) x}{\sigma^2} \right) \, dx \end{align*}

Example - Normal distribution

Moment generating function

We have shown \begin{equation} \tag{2} M_X(t) = \exp\left(-\frac{\mu^2}{2\sigma^2} \right) \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{\infty} \exp \left(- \frac{x^2}{2\sigma^2} + \frac{(t\sigma^2+\mu) x}{\sigma^2} \right) \, dx \end{equation} Replacing \mu by (t\sigma^2 + \mu) in (1) we obtain \begin{equation} \tag{3} \int_{-\infty}^{\infty} \exp \left(- \frac{x^2}{2\sigma^2} + \frac{(t\sigma^2+\mu) x}{\sigma^2} \right) \, dx = \exp \left( \frac{(t\sigma^2+\mu)^2}{2\sigma^2} \right) \, \frac{1}{\sqrt{2\pi}\sigma} \end{equation} Substituting (3) in (2) and simplifying we get M_X(t) = \exp \left( \mu t + \frac{t^2 \sigma^2}{2} \right)

Example - Normal distribution

Mean

Recall the mgf M_X(t) = \exp \left( \mu t + \frac{t^2 \sigma^2}{2} \right) The first derivative is M_X'(t) = (\mu + \sigma^2 t ) \exp \left( \mu t + \frac{t^2 \sigma^2}{2} \right) Therefore the mean: {\rm I\kern-.3em E}[X] = M_X'(0) = \mu

Example - Normal distribution

Variance

The first derivative of mgf is M_X'(t) = (\mu + \sigma^2 t ) \exp \left( \mu t + \frac{t^2 \sigma^2}{2} \right) The second derivative is then M_X''(t) = \sigma^2 \exp \left( \mu t + \frac{t^2 \sigma^2}{2} \right) + (\mu + \sigma^2 t )^2 \exp \left( \mu t + \frac{t^2 \sigma^2}{2} \right) Therefore the second moment is: {\rm I\kern-.3em E}[X^2] = M_X''(0) = \sigma^2 + \mu^2

Example - Normal distribution

Variance

We have seen that: {\rm I\kern-.3em E}[X] = \mu \quad \qquad {\rm I\kern-.3em E}[X^2] = \sigma^2 + \mu^2 Therefore the variance is: \begin{align*} {\rm Var}[X] & = {\rm I\kern-.3em E}[X^2] - {\rm I\kern-.3em E}[X]^2 \\ & = \sigma^2 + \mu^2 - \mu^2 \\ & = \sigma^2 \end{align*}

Example - Gamma distribution

Moment generating function

Suppose X \sim \Gamma(\alpha,\beta). This means f_X(x) = \begin{cases} \dfrac{x^{\alpha-1} e^{-\beta{x}} \beta^{\alpha}}{\Gamma(\alpha)} & \text{ if } x > 0 \\ 0 & \text{ if } x \leq 0 \end{cases}

• We have seen already that {\rm I\kern-.3em E}[X] = \frac{\alpha}{\beta} \quad \qquad {\rm Var}[X] = \frac{\alpha}{\beta^2}

• We want to compute mgf M_X to derive again {\rm I\kern-.3em E}[X] and {\rm Var}[X]

Example - Gamma distribution

Moment generating function

We compute \begin{align*} M_X(t) & = {\rm I\kern-.3em E}[e^{tX}] = \int_{-\infty}^\infty e^{tx} f_X(x) \, dx \\ & = \int_0^{\infty} e^{tx} \, \frac{x^{\alpha-1}e^{-\beta{x}} \beta^{\alpha}}{\Gamma(\alpha)} \, dx \\ & = \frac{\beta^{\alpha}}{\Gamma(\alpha)}\int_0^{\infty}x^{\alpha-1}e^{-(\beta-t)x} \, dx \end{align*}

Example - Gamma distribution

Moment generating function

From the previous slide we have M_X(t) = \frac{\beta^{\alpha}}{\Gamma(\alpha)}\int_0^{\infty}x^{\alpha-1}e^{-(\beta-t)x} \, dx Change variable y=(\beta-t)x and recall the definition of \Gamma: \begin{align*} \int_0^{\infty} x^{\alpha-1} e^{-(\beta-t)x} \, dx & = \int_0^{\infty} \frac{1}{(\beta-t)^{\alpha-1}} [(\beta-t)x]^{\alpha-1} e^{-(\beta-t)x} \frac{1}{(\beta-t)} (\beta - t) \, dx \\ & = \frac{1}{(\beta-t)^{\alpha}} \int_0^{\infty} y^{\alpha-1} e^{-y} \, dy \\ & = \frac{1}{(\beta-t)^{\alpha}} \Gamma(\alpha) \end{align*}

Example - Gamma distribution

Moment generating function

Therefore \begin{align*} M_X(t) & = \frac{\beta^{\alpha}}{\Gamma(\alpha)}\int_0^{\infty}x^{\alpha-1}e^{-(\beta-t)x} \, dx \\ & = \frac{\beta^{\alpha}}{\Gamma(\alpha)} \cdot \frac{1}{(\beta-t)^{\alpha}} \Gamma(\alpha) \\ & = \frac{\beta^{\alpha}}{(\beta-t)^{\alpha}} \end{align*}

Example - Gamma distribution

Expectation

From the mgf M_X(t) = \frac{\beta^{\alpha}}{(\beta-t)^{\alpha}} we compute the first derivative: \begin{align*} M_X'(t) & = \frac{d}{dt} [\beta^{\alpha}(\beta-t)^{-\alpha}] \\ & = \beta^{\alpha}(-\alpha)(\beta-t)^{-\alpha-1}(-1) \\ & = \alpha\beta^{\alpha}(\beta-t)^{-\alpha-1} \end{align*}

Example - Gamma distribution

Expectation

From the first derivative M_X'(t) = \alpha\beta^{\alpha}(\beta-t)^{-\alpha-1} we compute the expectation \begin{align*} {\rm I\kern-.3em E}[X] & = M_X'(0) \\ & = \alpha\beta^{\alpha}(\beta)^{-\alpha-1} \\ & =\frac{\alpha}{\beta} \end{align*}

Example - Gamma distribution

Variance

From the first derivative M_X'(t) = \alpha\beta^{\alpha}(\beta-t)^{-\alpha-1} we compute the second derivative \begin{align*} M_X''(t) & = \frac{d}{dt}[\alpha\beta^{\alpha}(\beta-t)^{-\alpha-1}] \\ & = \alpha\beta^{\alpha}(-\alpha-1)(\beta-t)^{-\alpha-2}(-1)\\ & = \alpha(\alpha+1)\beta^{\alpha}(\beta-t)^{-\alpha-2} \end{align*}

Example - Gamma distribution

Variance

From the second derivative M_X''(t) = \alpha(\alpha+1)\beta^{\alpha}(\beta-t)^{-\alpha-2} we compute the second moment: \begin{align*} {\rm I\kern-.3em E}[X^2] & = M_X''(0) \\ & = \alpha(\alpha+1)\beta^{\alpha}(\beta)^{-\alpha-2} \\ & = \frac{\alpha(\alpha + 1)}{\beta^2} \end{align*}

Example - Gamma distribution

Variance

From the first and second moments: {\rm I\kern-.3em E}[X] = \frac{\alpha}{\beta} \qquad \qquad {\rm I\kern-.3em E}[X^2] = \frac{\alpha(\alpha + 1)}{\beta^2} we can compute the variance \begin{align*} {\rm Var}[X] & = {\rm I\kern-.3em E}[X^2] - {\rm I\kern-.3em E}[X]^2 \\ & = \frac{\alpha(\alpha + 1)}{\beta^2} - \frac{\alpha^2}{\beta^2} \\ & = \frac{\alpha}{\beta^2} \end{align*}

Moment generating function

The mgf characterizes a distribution

Theorem

Let X and Y be random variables with mgfs M_X and M_Y respectively. Assume there exists \varepsilon>0 such that M_X(t) = M_Y(t) \,, \quad \forall \, t \in (-\varepsilon, \varepsilon) Then X and Y have the same cdf F_X(u) = F_Y(u) \,, \quad \forall \, x \in \mathbb{R}

In other words: \qquad same mgf \quad \implies \quad same distribution

Example

• Suppose X is a random variable such that M_X(t) = \exp \left( \mu t + \frac{t^2 \sigma^2}{2} \right) As the above is the mgf of a normal distribution, by the previous Theorem we infer X \sim N(\mu,\sigma^2)

• Suppose Y is a random variable such that M_Y(t) = \frac{\beta^{\alpha}}{(\beta-t)^{\alpha}} As the above is the mgf of a Gamma distribution, by the previous Theorem we infer Y \sim \Gamma(\alpha,\beta)

Part 5:
Probability revision II

Probability revision II

• You are expected to be familiar with the main concepts from Y1 module
  Introduction to Probability & Statistics

• Self-contained revision material available in Appendix A

Topics to review: Sections 4–5 of Appendix A

• Random vectors
• Bivariate vectors
• Joint pdf and pmf
• Marginals

• Conditional distributions
• Conditional expectation
• Conditional variance

Univariate vs Bivariate vs Multivariate

• Probability models seen so far only involve 1 random variable
  • These are called univariate models
• We are also interested in probability models involving multiple variables:
  • Models with 2 random variables are called bivariate
  • Models with more than 2 random variables are called multivariate

Random vectors

Definition

Recall: a random variable is a measurable function X \colon \Omega \to \mathbb{R}\,, \quad \Omega \,\, \text{ sample space}

Definition

A random vector is a measurable function \mathbf{X}\colon \Omega \to \mathbb{R}^n. We say that

• \mathbf{X} is univariate if n=1
• \mathbf{X} is bivariate if n=2
• \mathbf{X} is multivariate if n \geq 3

Random vectors

Notation

• The components of a random vector \mathbf{X} are denoted by \mathbf{X}= (X_1, \ldots, X_n) with X_i \colon \Omega \to \mathbb{R} random variables

• We denote a two-dimensional bivariate random vector by (X,Y) with X,Y \colon \Omega \to \mathbb{R} random variables

Summary - Bivariate Random Vectors

(X,Y) discrete random vector	(X,Y) continuous random vector
X and Y discrete RV	X and Y continuous RV
Joint pmf	Joint pdf
f_{X,Y}(x,y) := P(X=x,Y=y)	P((X,Y) \in A) = \int_A f_X(x,y) \,dxdy
f_{X,Y} \geq 0	f_{X,Y} \geq 0
\sum_{(x,y)\in \mathbb{R}^2} f_{X,Y}(x,y)=1	\int_{\mathbb{R}^2} f_{X,Y}(x,y) \, dxdy= 1
Marginal pmfs	Marginal pdfs
f_X (x) := P(X=x)	P(a \leq X \leq b) = \int_a^b f_X(x) \,dx
f_Y (y) := P(Y=y)	P(a \leq Y \leq b) = \int_a^b f_Y(y) \,dy
f_X (x)=\sum_{y \in \mathbb{R}} f_{X,Y}(x,y)	f_X(x) = \int_{\mathbb{R}} f_{X,Y}(x,y) \,dy
f_Y (y)=\sum_{x \in \mathbb{R}} f_{X,Y}(x,y)	f_Y(y) = \int_{\mathbb{R}} f_{X,Y}(x,y) \,dx

Expected Value

• Suppose (X,Y) \colon \Omega \to \mathbb{R}^2 is random vector and g \colon \mathbb{R}^2 \to \mathbb{R} function
• Then g(X,Y) \colon \Omega \to \mathbb{R} is random variable

Definition

The expected value of the random variable g(X,Y) is \begin{align*} {\rm I\kern-.3em E}[g(X,Y)] & := \sum_{x,y} g(x,y) P(X=x,Y=y) \quad \text{ if } (X,Y) \text{ discrete} \\ {\rm I\kern-.3em E}[g(X,Y)] & := \int_{\mathbb{R}^2} g(x,y) f_{X,Y}(x,y) \, dxdy \quad \text{ if } (X,Y) \text{ continuous} \end{align*}

Notation:The symbol \int_{\mathbb{R}^2} denotes the double integral \int_{-\infty}^\infty\int_{-\infty}^\infty

Conditional distributions

(X,Y) rv with joint pdf (or pmf) f_{X,Y} and marginal pdfs (or pmfs) f_X, f_Y

• The conditional pdf (or pmf) of Y given that X=x is the function f(\cdot | x) f(y|x) := \frac{f_{X,Y}(x,y)}{f_X(x)} \, , \qquad \text{ whenever} \quad f_X(x)>0

• The conditional pdf (or pmf) of X given that Y=y is the function f(\cdot | y) f(x|y) := \frac{f_{X,Y}(x,y)}{f_Y(y)}\, , \qquad \text{ whenever} \quad f_Y(y)>0

• Notation: We will often write

  • Y|X to denote the distribution f(y|x)
  • X|Y to denote the distribution f(x|y)

Conditional expectation

Definition

(X,Y) random vector and g \colon \mathbb{R}\to \mathbb{R} function. The conditional expectation of g(Y) given X=x is \begin{align*} {\rm I\kern-.3em E}[g(Y) | x] & := \sum_{y} g(y) f(y|x) \quad \text{ if } (X,Y) \text{ discrete} \\ {\rm I\kern-.3em E}[g(Y) | x] & := \int_{y \in \mathbb{R}} g(y) f(y|x) \, dy \quad \text{ if } (X,Y) \text{ continuous} \end{align*}

• {\rm I\kern-.3em E}[g(Y) | x] is a real number for all x \in \mathbb{R}
• {\rm I\kern-.3em E}[g(Y) | X] denotes the Random Variable h(X) where h(x):={\rm I\kern-.3em E}[g(Y) | x]

Conditional variance

Definition

(X,Y) random vector. The conditional variance of Y given X=x is {\rm Var}[Y | x] := {\rm I\kern-.3em E}[Y^2|x] - {\rm I\kern-.3em E}[Y|x]^2

• {\rm Var}[Y | x] is a real number for all x \in \mathbb{R}
• {\rm Var}[Y | X] denotes the Random Variable {\rm Var}[Y | X] := {\rm I\kern-.3em E}[Y^2|X] - {\rm I\kern-.3em E}[Y|X]^2

Exercise - Conditional distribution

Assume given a continuous random vector (X,Y) with joint pdf f_{X,Y}(x,y) := e^{-y} \,\, \text{ if } \,\, 0 < x < y \,, \quad f_{X,Y}(x,y) :=0 \,\, \text{ otherwise}

• Compute f_X and f(y|x)
• Compute {\rm I\kern-.3em E}[Y|X]
• Compute {\rm Var}[Y|X]

Solution

• We compute f_X, the marginal pdf of X:
  • If x \leq 0 then f_{X,Y}(x,y)=0. Therefore f_X(x) = \int_{-\infty}^\infty f_{X,Y}(x,y) \, dy = 0
  • If x > 0 then f_{X,Y}(x,y)=e^{-y} if y>x, and f_{X,Y}(x,y)=0 if y \leq x. Thus \begin{align*} f_X(x) & = \int_{-\infty}^\infty f_{X,Y}(x,y) \, dy = \int_{x}^\infty e^{-y} \, dy \\ & = - e^{-y} \bigg|_{y=x}^{y=\infty} = -e^{-\infty} + e^{-x} = e^{-x} \end{align*}

Solution

• The marginal pdf of X has then exponential distribution f_{X}(x) = \begin{cases} e^{-x} & \text{ if } x > 0 \\ 0 & \text{ if } x \leq 0 \end{cases}

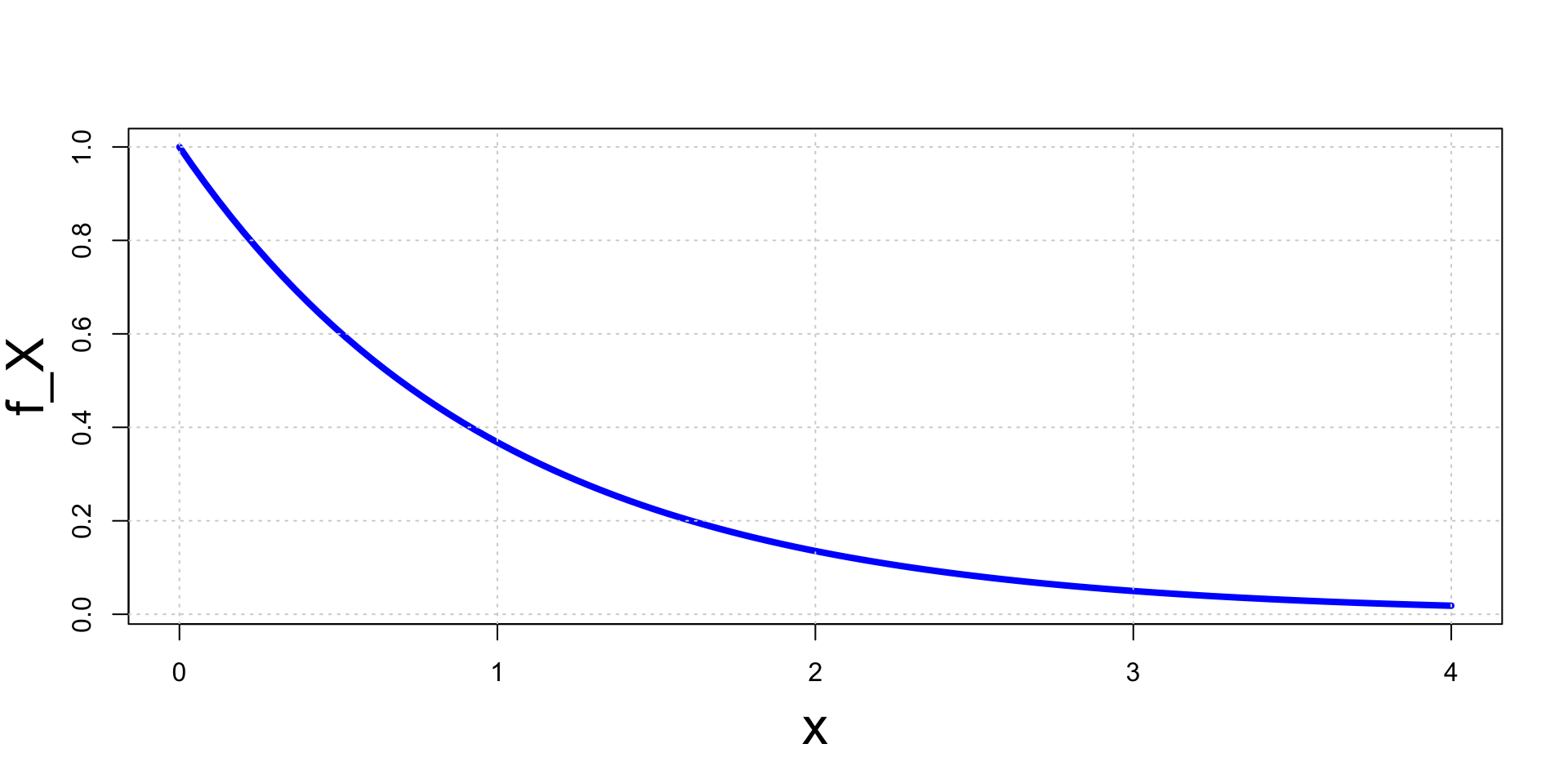
Solution

• We now compute f(y|x), the conditional pdf of Y given X=x:
  • Note that f_X(x)>0 for all x>0
  • Hence assume fixed some x>0
  • If y>x we have f_{X,Y}(x,y)=e^{-y}. Hence f(y|x) := \frac{f_{X,Y}(x,y)}{f_X(x)} = \frac{e^{-y}}{e^{-x}} = e^{-(y-x)}
  • If y \leq x we have f_{X,Y}(x,y)=0. Hence f(y|x) := \frac{f_{X,Y}(x,y)}{f_X(x)} = \frac{0}{e^{-x}} = 0

Solution

• The conditional distribution Y|X is therefore exponential f(y|x) = \begin{cases} e^{-(y-x)} & \text{ if } y > x \\ 0 & \text{ if } y \leq x \end{cases}

• The conditional expectation of Y given X=x is \begin{align*} {\rm I\kern-.3em E}[Y|x] & = \int_{-\infty}^\infty y f(y|x) \, dy = \int_{x}^\infty y e^{-(y-x)} \, dy \\ & = -(y+1) e^{-(y-x)} \bigg|_{x}^\infty = x + 1 \end{align*} where we integrated by parts

Solution

• Therefore conditional expectation of Y given X=x is {\rm I\kern-.3em E}[Y|x] = x + 1

• This can also be interpreted as the random variable {\rm I\kern-.3em E}[Y|X] = X + 1

Solution

• The conditional second moment of Y given X=x is \begin{align*} {\rm I\kern-.3em E}[Y^2|x] & = \int_{-\infty}^\infty y^2 f(y|x) \, dy = \int_{x}^\infty y^2 e^{-(y-x)} \, dy \\ & = (y^2+2y+2) e^{-(y-x)} \bigg|_{x}^\infty = x^2 + 2x + 2 \end{align*} where we integrated by parts

• The conditional variance of Y given X=x is {\rm Var}[Y|x] = {\rm I\kern-.3em E}[Y^2|x] - {\rm I\kern-.3em E}[Y|x]^2 = x^2 + 2x + 2 - (x+1)^2 = 1

• This can also be interpreted as the random variable {\rm Var}[Y|X] = 1

Conditional Expectation

A useful formula

Theorem

(X,Y) random vector. Then {\rm I\kern-.3em E}[X] = {\rm I\kern-.3em E}[ {\rm I\kern-.3em E}[X|Y] ]

Note: The above formula contains abuse of notation – {\rm I\kern-.3em E} has 3 meanings

• First {\rm I\kern-.3em E} is with respect to the marginal of X
• Second {\rm I\kern-.3em E} is with respect to the marginal of Y
• Third {\rm I\kern-.3em E} is with respect to the conditional distribution X|Y

Conditional Variance

A useful formula

Theorem

(X,Y) random vector. Then {\rm Var}[X] = {\rm I\kern-.3em E}[ {\rm Var}[ X|Y] ] + {\rm Var}[{\rm I\kern-.3em E}[X|Y]]

Exercise: Suppose that the distribution of Y, conditional on X = x, is N(x, x^2). Suppose X is uniform on [0,1].

• Compute {\rm I\kern-.3em E}[Y]
• Compute {\rm Var}[Y]

Conditional Variance

Solution

• By assumption X is uniform on [0,1]. Therefore \begin{align*} f_X(x) & = \chi_{[0,1]}(x) = \begin{cases} 1 & \, \text{ if } \, x \in [0,1] \\ 0 & \, \text{ otherwise } \end{cases} \\ {\rm I\kern-.3em E}[X] & = \int_\mathbb{R}x f_{X}(x)\, dx = \int_0^1 x \, dx = \frac12 \\ {\rm I\kern-.3em E}[X^2] & = \int_\mathbb{R}x^2 f_{X} (x)\, dx = \int_0^1 x^2 \, dx = \frac13 \\ {\rm Var}[X] & = {\rm I\kern-.3em E}[X^2] - {\rm I\kern-.3em E}[X]^2 = \frac13 - \frac{1}{4} = \frac{1}{12} \end{align*}

Conditional Variance

Solution

• By assumption Y | X = x is N(x,x^2). Therefore {\rm I\kern-.3em E}[Y|X] = X \,, \qquad {\rm Var}[Y|X] = X^2

• Therefore we conclude \begin{align*} {\rm I\kern-.3em E}[Y] & = {\rm I\kern-.3em E}[ {\rm I\kern-.3em E}[Y|X] ] = {\rm I\kern-.3em E}[X] = \frac12 \\ & \phantom{s} \\ {\rm Var}[Y] & = {\rm I\kern-.3em E}[{\rm Var}[Y|X]] + {\rm Var}[{\rm I\kern-.3em E}[Y|X]] \\ & = {\rm Var}[X] + {\rm I\kern-.3em E}[X^2] \\ & = \frac{1}{12} + \frac13 = \frac{5}{12} \end{align*}

References

[1]

Bingham, Nicholas H., Fry, John M., Regression, linear models in statistics, Springer, 2010.

[2]

Fry, John M., Burke, Matt, Quantitative methods in finance using R, Open University Press, 2022.

[3]

Casella, George, Berger, Roger L., Statistical inference, second edition, Brooks/Cole, 2002.

[4]

DeGroot, Morris H., Schervish, Mark J., Probability and statistics, Fourth Edition, Addison-Wesley, 2012.

[5]

Dalgaard, Peter, Introductory statistics with R, Second Edition, Springer, 2008.

[6]

Davies, Tilman M., The book of R, No Starch Press, 2016.