Statistical Models

Lecture 8

Dr. Silvio Fanzon
S.Fanzon@hull.ac.uk

University of Hull

Dr. John Fry
J.M.Fry@hull.ac.uk

University of Hull

Lecture 8:
The maths of
regression

Outline of Lecture 8

  1. Least squares
  2. Simple linear regression

Part 1:
Least squares

Example: Blood Pressure

10 patients are treated with Drug A and Drug B

  • These drugs cause change in blood pressure
  • Patients are given the drugs one at a time
  • Changes in blood pressure are recorded
  • For patient i we denote by
    • x_i the change caused by Drug A
    • y_i the change caused by Drug B
i x_i y_i
1 1.9 0.7
2 0.8 -1.0
3 1.1 -0.2
4 0.1 -1.2
5 -0.1 -0.1
6 4.4 3.4
7 4.6 0.0
8 1.6 0.8
9 5.5 3.7
10 3.4 2.0

Example: Blood Pressure

Goal:

  • Predict reaction to Drug B, knowing reaction to Drug A
  • This means predict y_i from x_i

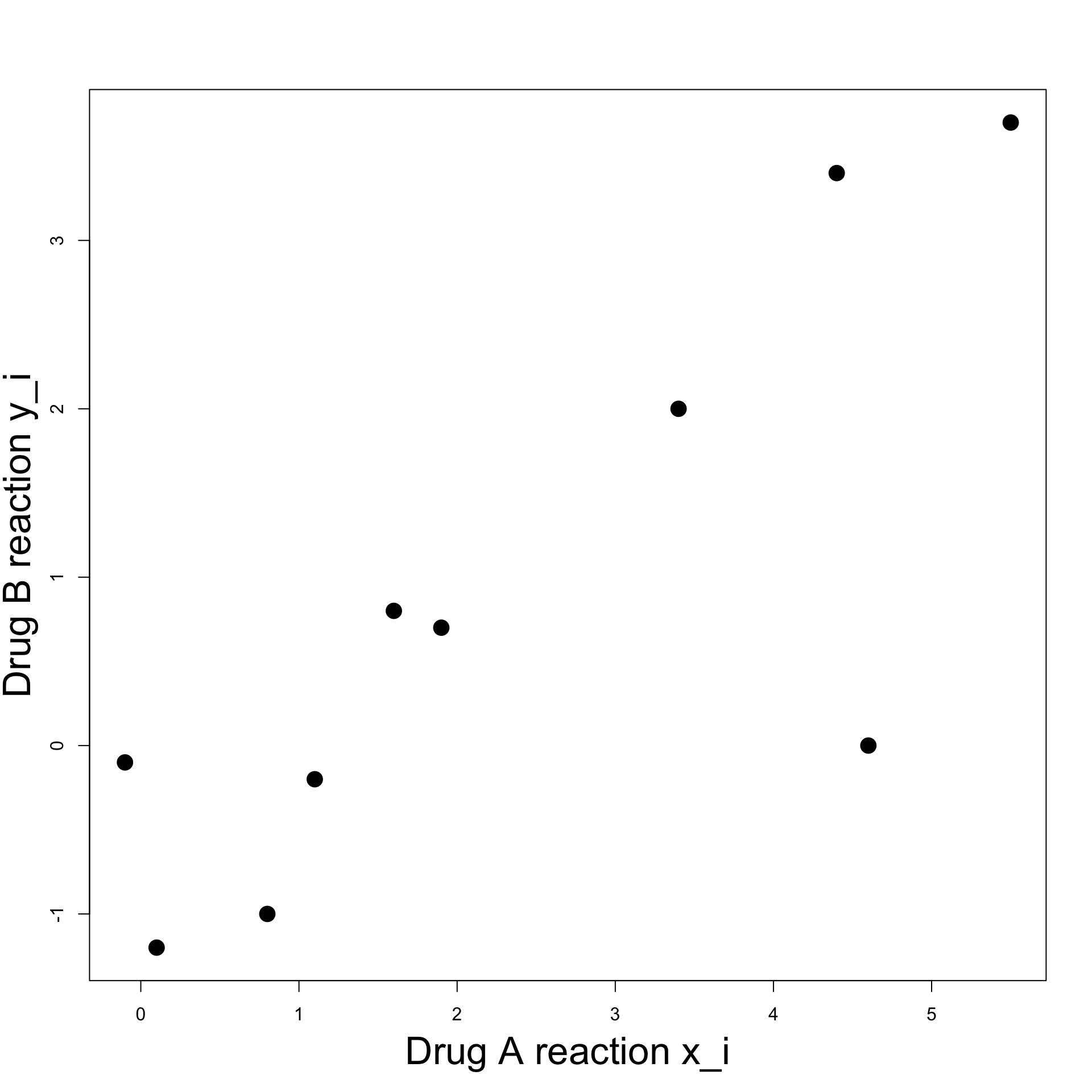
Plot:

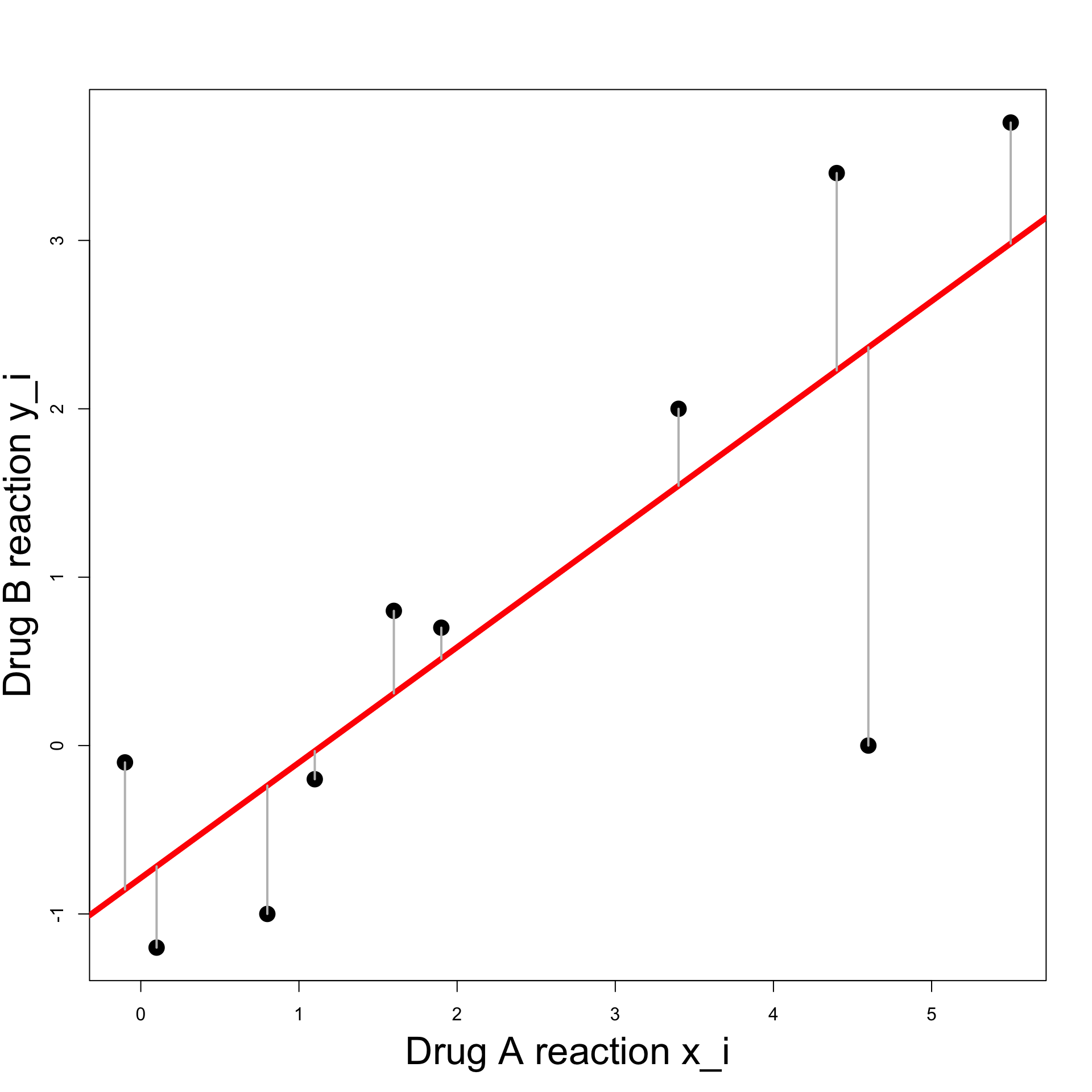
  • To visualize data we can plot pairs (x_i,y_i)
  • Points seem to align
  • It seems there is a linear relation between x_i and y_i

Example: Blood Pressure

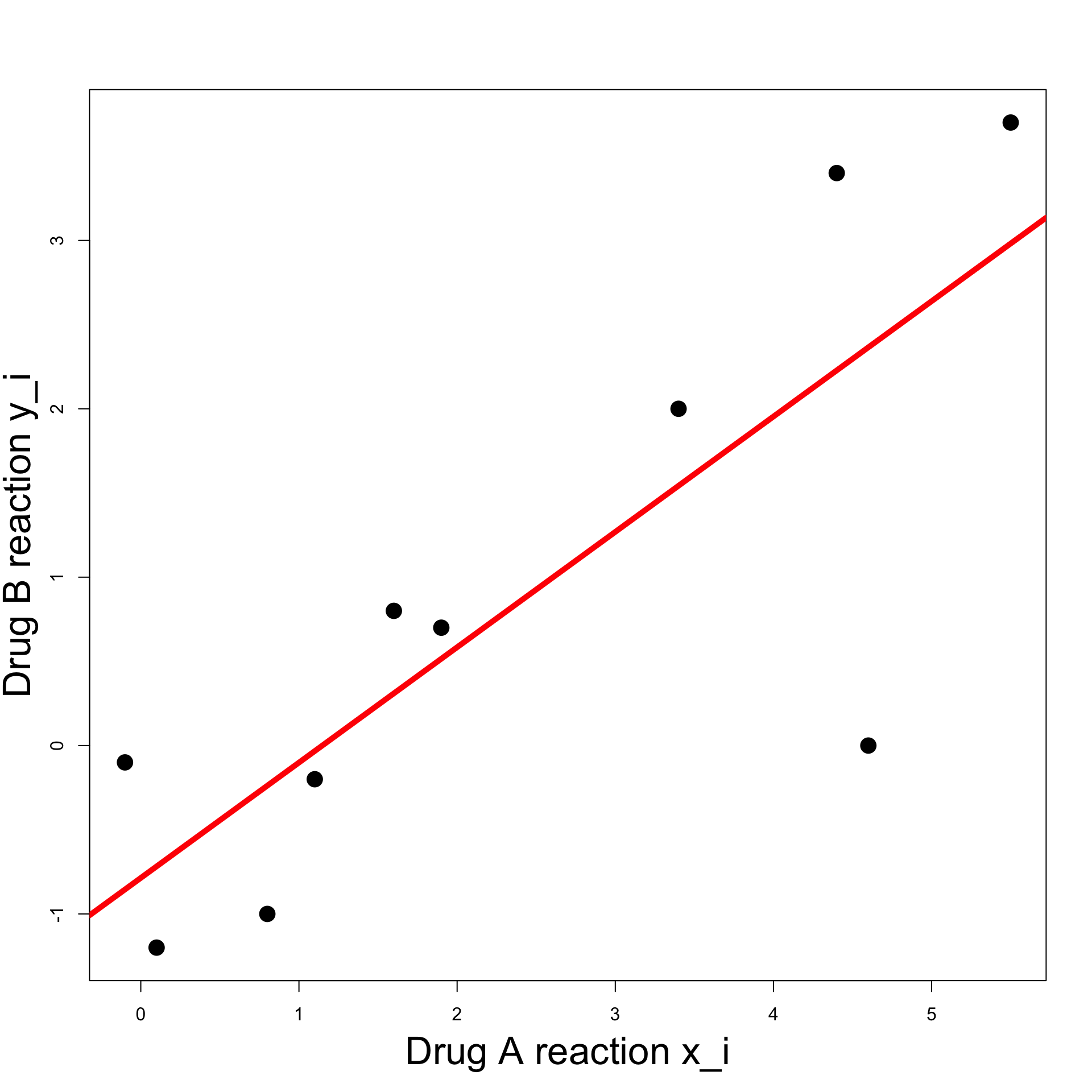
Linear relation:

  • Try to fit a line through the data
  • Line roughly predicts y_i from x_i
  • However note the outlier (x_7,y_7) = (4.6, 0)
  • How is such line constructed?

Example: Blood Pressure

Least Squares Line:

  • A general line has equation y = \beta x + \alpha for some
    • slope \beta
    • intercept \alpha
  • Value predicted by the line for x_i is \hat{y}_i = \beta x_i + \alpha

Example: Blood Pressure

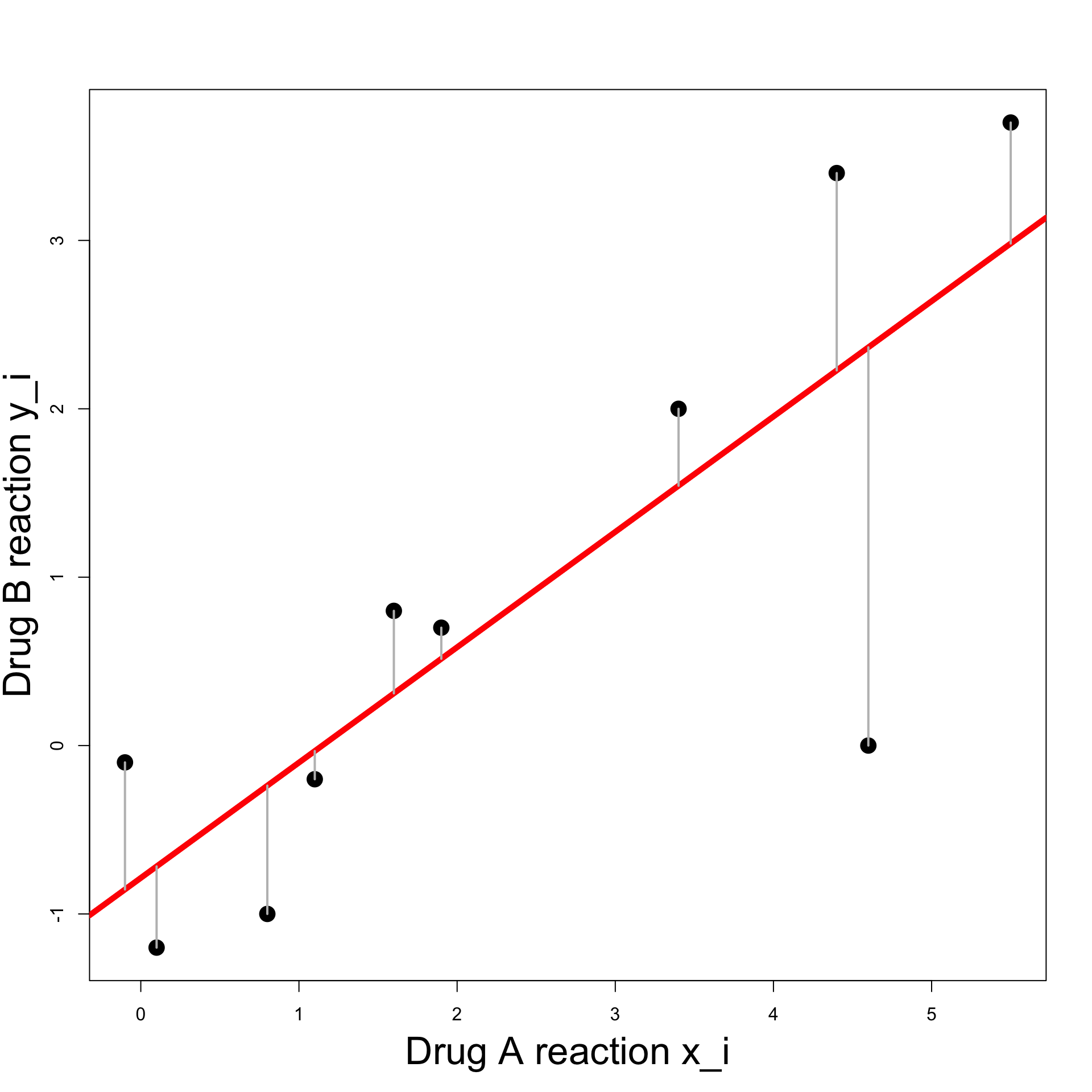
Least Squares Line:

  • We would like predicted and actual value to be close \hat{y}_i \approx y_i

  • Hence the vertical difference has to be small y_i - \hat{y}_i \approx 0

Example: Blood Pressure

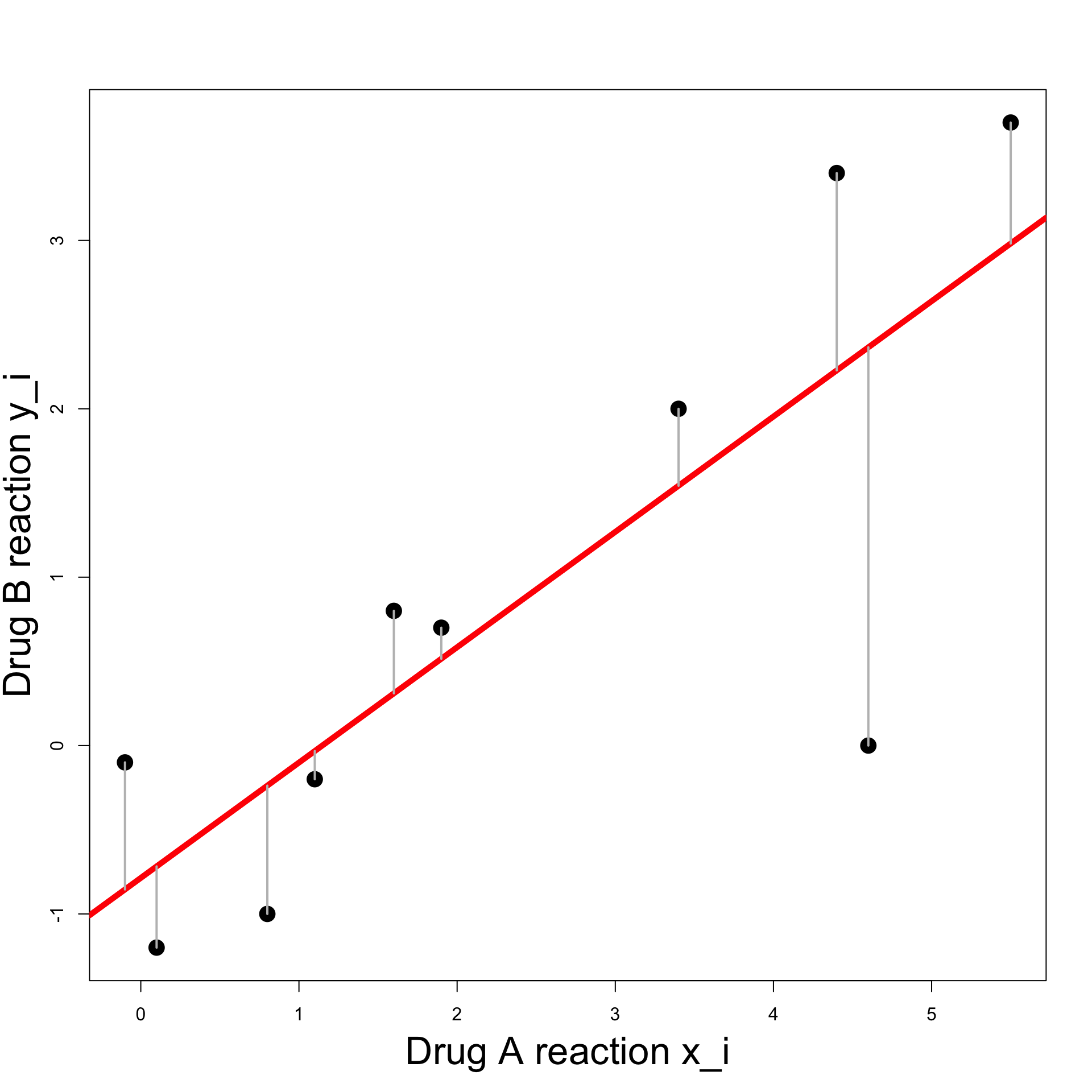
Least Squares Line:

  • We want \hat{y}_i \approx y_i \,, \qquad \forall \, i

  • A way to ensure the above is by minimizing the sum of squares \min_{\alpha, \beta} \ \sum_{i} \ (y_i - \hat{y}_i)^2 \hat{y}_i = \beta x_i + \alpha

Residual Sum of Squares

Definition
Let (x_1,y_1), \ldots, (x_n, y_n) be a set of n points. Consider the line y = \beta x + \alpha The Residual Sum of Squares associated to the line is \mathop{\mathrm{RSS}}(\alpha,\beta) := \sum_{i=1}^n (y_i-\alpha-{\beta}x_i)^2

Note: \mathop{\mathrm{RSS}} can be seen as a function \mathop{\mathrm{RSS}}\colon \mathbb{R}^2 \to \mathbb{R}\qquad \quad \mathop{\mathrm{RSS}}= \mathop{\mathrm{RSS}}(\alpha,\beta)

\mathop{\mathrm{RSS}}(\alpha,\beta) for Blood Pressure data

Summary statistics

Suppose given the sample (x_1,y_1), \ldots, (x_n, y_n)

  • We want to minimize the associated RSS \min_{\alpha,\beta} \ \mathop{\mathrm{RSS}}(\alpha,\beta) = \min_{\alpha,\beta} \ \sum_{i=1}^n (y_i-\alpha-{\beta}x_i)^2

  • To this end we define the following quantities

Summary statistics

Suppose given the sample (x_1,y_1), \ldots, (x_n, y_n)

  • Sample Means: \overline{x} := \frac{1}{n} \sum_{i=1}^n x_i \qquad \quad \overline{y} := \frac{1}{n} \sum_{i=1}^n y_i

  • Sums of squares: S_{xx} := \sum_{i=1}^n ( x_i - \overline{x} )^2 \qquad \quad S_{yy} := \sum_{i=1}^n ( y_i - \overline{y} )^2

Summary statistics

Suppose given the sample (x_1,y_1), \ldots, (x_n, y_n)

  • Sum of cross-products: S_{xy} := \sum_{i=1}^n ( x_i - \overline{x} ) ( y_i - \overline{y} )

Minimizing the RSS

Theorem

Let (x_1,y_1), \ldots, (x_n, y_n) be a set of n points. Consider the minimization problem \begin{equation} \tag{M} \min_{\alpha,\beta } \ \mathop{\mathrm{RSS}}= \min_{\alpha,\beta} \ \sum_{i=1}^n (y_i-\alpha-{\beta}x_i)^2 \end{equation} Then

  1. There exists a unique line solving (M)
  2. Such line has the form y = \hat{\beta} x + \hat{\alpha} with \hat{\beta} = \frac{S_{xy}}{S_{xx}} \qquad \qquad \hat{\alpha} = \overline{y} - \hat{\beta} \ \overline{x}

Positive semi-definite matrix

To prove the Theorem we need some background results

  • A symmetric matrix is positive semi-definite if all the eigenvalues \lambda_i satisfy \lambda_i \geq 0

  • Proposition: A 2 \times 2 symmetric matrix M is positive semi-definite iff \det M \geq 0 \,, \qquad \quad \operatorname{Tr}(M) \geq 0

Positive semi-definite Hessian

  • Suppose given a smooth function of 2 variables

f \colon \mathbb{R}^2 \to \mathbb{R}\qquad \quad f = f (x,y)

  • The Hessian of f is the matrix

\nabla^2 f = \left( \begin{array}{cc} f_{xx} & f_{xy} \\ f_{yx} & f_{yy} \\ \end{array} \right)

Positive semi-definite Hessian

  • In particular the Hessian is positive semi-definite iff

\det \nabla^2 f = f_{xx} f_{yy} - f_{xy}^2 \geq 0 \qquad \quad f_{xx} + f_{yy} \geq 0

  • Side Note: For C^2 functions it holds that

\nabla^2 f \, \text{ is positive semi-definite} \qquad \iff \qquad f \, \text{ is convex}

Optimality conditions

Lemma

Suppose f \colon \mathbb{R}^2 \to \mathbb{R} has positive semi-definite Hessian. They are equivalent

  1. The point (\hat{x},\hat{y}) is a minimizer of f, that is, f(\hat{x}, \hat{y}) = \min_{x,y} \ f(x,y)

  2. The point (\hat{x},\hat{y}) satisfies the optimality conditions \nabla f (\hat{x},\hat{y}) = 0

Note: The proof of the above Lemma can be found in [1]

Optimality conditions

Example

  • The main example of strictly convex function in 2D is

f(x,y) = x^2 + y^2

  • It is clear that

\min_{x,y} \ f(x,y) = \min_{x,y} \ x^2 + y^2 = 0 with the only minimizer being (0,0)

  • However let us use the Lemma to prove this fact

Optimality conditions

Example

  • The gradient of f = x^2 + y^2 is

\nabla f = (f_x,f_y) = (2x, 2y)

  • Therefore the optimality condition has unique solution

\nabla f = 0 \qquad \iff \qquad x = y = 0

Optimality conditions

Example

  • The Hessian of f is

\nabla^2 f = \left( \begin{array}{cc} f_{xx} & f_{xy} \\ f_{yx} & f_{yy} \end{array} \right) = \left( \begin{array}{cc} 2 & 0 \\ 0 & 2 \end{array} \right)

  • The Hessian is positive semi-definite since

\det \nabla^2 f = 4 > 0 \qquad \qquad f_{xx} + f_{yy} = 4 > 0

  • By the Lemma we conclude that (0,0) is the unique minimizer of f, that is,

0 = f(0,0) = \min_{x,y} \ f(x,y)

Minimizing the RSS

Proof of Theorem

  • We go back to proving the RSS Minimization Theorem

  • Suppose given data points (x_1,y_1), \ldots, (x_n, y_n)

  • We want to solve the minimization problem

\begin{equation} \tag{M} \min_{\alpha,\beta } \ \mathop{\mathrm{RSS}}= \min_{\alpha,\beta} \ \sum_{i=1}^n (y_i-\alpha-{\beta}x_i)^2 \end{equation}

  • In order to use the Lemma we need to compute

\nabla \mathop{\mathrm{RSS}}\quad \text{ and } \quad \nabla^2 \mathop{\mathrm{RSS}}

Minimizing the RSS

Proof of Theorem

  • We first compute \nabla \mathop{\mathrm{RSS}} and solve the optimality conditions \nabla \mathop{\mathrm{RSS}}(\alpha,\beta) = 0

  • To this end, recall that \overline{x} := \frac{\sum_{i=1}^nx_i}{n} \qquad \implies \qquad \sum_{i=1}^n x_i = n \overline{x}

  • Similarly we have \sum_{i=1}^n y_i = n \overline{y}

Minimizing the RSS

Proof of Theorem

  • Therefore we get

\begin{align*} \mathop{\mathrm{RSS}}_{\alpha} & = -2\sum_{i=1}^n(y_i- \alpha- \beta x_i) \\[10pt] & = - 2 n \overline{y} + 2n \alpha + 2 \beta n \overline{x} \\[20pt] \mathop{\mathrm{RSS}}_{\beta} & = -2\sum_{i=1}^n x_i (y_i- \alpha - \beta x_i) \\[10pt] & = - 2 \sum_{i=1}^n x_i y_i + 2 \alpha n \overline{x} + 2 \beta \sum_{i=1}^n x_i^2 \end{align*}

Minimizing the RSS

Proof of Theorem

  • Hence the optimality conditions are

\begin{align} - 2 n \overline{y} + 2n \alpha + 2 \beta n \overline{x} & = 0 \tag{1} \\[20pt] - 2 \sum_{i=1}^n x_i y_i + 2 \alpha n \overline{x} + 2 \beta \sum_{i=1}^n x_i^2 & = 0 \tag{2} \end{align}

Minimizing the RSS

Proof of Theorem

  • Equation (1) is

-2 n \overline{y} + 2n \alpha + 2 \beta n \overline{x} = 0

  • By simplifying and rearraging, we find that (1) is equivalent to

\alpha = \overline{y}- \beta \overline{x}

Minimizing the RSS

Proof of Theorem

  • Equation (2) is equivalent to

\sum_{i=1}^n x_i y_i - \alpha n \overline{x} - \beta \sum_{i=1}^n x^2_i = 0

  • From the previous slide we have \alpha = \overline{y}- \beta \overline{x}

Minimizing the RSS

Proof of Theorem

  • Substituting in Equation (2) we get \begin{align*} 0 & = \sum_{i=1}^n x_i y_i - \alpha n \overline{x} - \beta \sum_{i=1}^n x^2_i \\ & = \sum_{i=1}^n x_i y_i - n \overline{x} \, \overline{y} + \beta n \overline{x}^2 - \beta \sum_{i=1}^n x^2_i \\ & = \sum_{i=1}^n (x_i y_i - \overline{x} \, \overline{y} ) - \beta \left( \sum_{i=1}^n x^2_i - n\overline{x}^2 \right) = S_{xy} - \beta S_{xx} \end{align*} where we used the usual identity S_{xx} = \sum_{i=1}^n ( x_i - \overline{x})^2 = \sum_{i=1}^n x_i^2 - n\overline{x}^2

Minimizing the RSS

Proof of Theorem

  • Hence Equation (2) is equivalent to \beta = \frac{S_{xy}}{ S_{xx} }

  • Also recall that Equation (1) is equivalent to \alpha = \overline{y}- \beta \overline{x}

  • Therefore (\hat\alpha, \hat\beta) solves the optimality conditions \nabla \mathop{\mathrm{RSS}}= 0 iff \hat\alpha = \overline{y}- \hat\beta \overline{x} \,, \qquad \quad \hat\beta = \frac{S_{xy}}{ S_{xx} }

Minimizing the RSS

Proof of Theorem

  • We need to compute \nabla^2 \mathop{\mathrm{RSS}}

  • To this end recall that \mathop{\mathrm{RSS}}_{\alpha} = - 2 n \overline{y} + 2n \alpha + 2 \beta n \overline{x} \,, \quad \mathop{\mathrm{RSS}}_{\beta} = - 2 \sum_{i=1}^n x_i y_i + 2 \alpha n \overline{x} + 2 \beta \sum_{i=1}^n x_i^2

  • Therefore we have \begin{align*} \mathop{\mathrm{RSS}}_{\alpha \alpha} & = 2n \qquad & \mathop{\mathrm{RSS}}_{\alpha \beta} & = 2 n \overline{x} \\ \mathop{\mathrm{RSS}}_{\beta \alpha } & = 2 n \overline{x} \qquad & \mathop{\mathrm{RSS}}_{\beta \beta} & = 2 \sum_{i=1}^{n} x_i^2 \end{align*}

Minimizing the RSS

Proof of Theorem

  • The Hessian determinant is

\begin{align*} \det \nabla^2 \mathop{\mathrm{RSS}}& = \mathop{\mathrm{RSS}}_{\alpha \alpha}\mathop{\mathrm{RSS}}_{\beta \beta} - \mathop{\mathrm{RSS}}_{\alpha \beta}^2 \\[10pt] & = 4n \sum_{i=1}^{n} x_i^2 - 4 n^2 \overline{x}^2 \\[10pt] & = 4n \left( \sum_{i=1}^{n} x_i^2 - n \overline{x}^2 \right) \\[10pt] & = 4n S_{xx} \end{align*}

Minimizing the RSS

Proof of Theorem

  • Recall that

S_{xx} = \sum_{i=1}^n (x_i - \overline{x})^2 \geq 0

  • Therefore we have

\det \nabla^2 \mathop{\mathrm{RSS}}= 4n S_{xx} \geq 0

Minimizing the RSS

Proof of Theorem

  • We also have

\mathop{\mathrm{RSS}}_{\alpha \alpha} + \mathop{\mathrm{RSS}}_{\beta \beta} = 2n + 2 \sum_{i=1}^{n} x_i^2 \geq 0

  • Therefore we have proven \det \nabla^2 \mathop{\mathrm{RSS}}\geq 0 \,, \qquad \quad \mathop{\mathrm{RSS}}_{\alpha \alpha} + \mathop{\mathrm{RSS}}_{\beta \beta} \geq 0

  • As the Hessian is symmetric, we conclude that \nabla^2 \mathop{\mathrm{RSS}} is positive semi-definite

Minimizing the RSS

Proof of Theorem

  • By the Lemma we have that all the solutions (\alpha,\beta) to the optimality conditions \nabla \mathop{\mathrm{RSS}}(\alpha,\beta) = 0 are minimizers

  • Therefore (\hat \alpha,\hat\beta) with \hat\alpha = \overline{y}- \hat\beta \overline{x} \,, \qquad \quad \hat\beta = \frac{S_{xy}}{ S_{xx} } is a minimizer of \mathop{\mathrm{RSS}}, ending the proof

Least-squares line

The previous Theorem allows to give the following definition

Definition
Let (x_1,y_1), \ldots, (x_n, y_n) be a set of n points. The least-squares line is the line y = \hat\beta x + \hat \alpha where we define \hat{\alpha} = \overline{y} - \hat{\beta} \ \overline{x} \qquad \qquad \hat{\beta} = \frac{S_{xy}}{S_{xx}}

Exercise: Blood Pressure

Computing the least-squares line in R

In R do the following:

  • Input the data into a data-frame

  • Plot the data points (x_i,y_i)

  • Compute the least-square line coefficients \hat{\alpha} = \overline{y} - \hat{\beta} \ \overline{x} \qquad \qquad \hat{\beta} = \frac{S_{xy}}{S_{xx}}

  • Plot the least squares line

i x_i y_i
1 1.9 0.7
2 0.8 -1.0
3 1.1 -0.2
4 0.1 -1.2
5 -0.1 -0.1
6 4.4 3.4
7 4.6 0.0
8 1.6 0.8
9 5.5 3.7
10 3.4 2.0

Exercise: Blood Pressure

First Solution

  • We give a first solution using elementary R functions

  • The code to input the data into a data-frame is as follows

# Input blood pressure changes data into data-frame

changes <- data.frame(drug_A = c(1.9, 0.8, 1.1, 0.1, -0.1, 
                                 4.4, 4.6, 1.6, 5.5, 3.4),
                      drug_B = c(0.7, -1.0, -0.2, -1.2, -0.1, 
                                 3.4, 0.0, 0.8, 3.7, 2.0)
                     )
  • To shorten the code we assign drug_A and drug_B to vectors x and y
# Assign data-frame columns to vectors x and y
x <- changes$drug_A
y <- changes$drug_B

Exercise: Blood Pressure

First Solution

  • We compute averages \overline{x}, \overline{y} and covariances S_{xx}, S_{xy}
# Compute averages xbar and ybar
xbar <- mean(x)
ybar <- mean(y)

# Compute covariances S_xx and S_xy
S_xx <- var(x)
S_xy <- cov(x,y)

Exercise: Blood Pressure

First Solution

  • Compute the least-square line coefficients \hat{\alpha} = \overline{y} - \hat{\beta} \ \overline{x} \qquad \qquad \hat{\beta} = \frac{S_{xy}}{S_{xx}} 
# Compute least-square line coefficients
beta <- S_xy / S_xx
alpha <- ybar - beta * xbar
  • The coefficients computed by the above code are

Coefficient alpha = -0.7861478

Coefficient beta = 0.685042

Exercise: Blood Pressure

First Solution

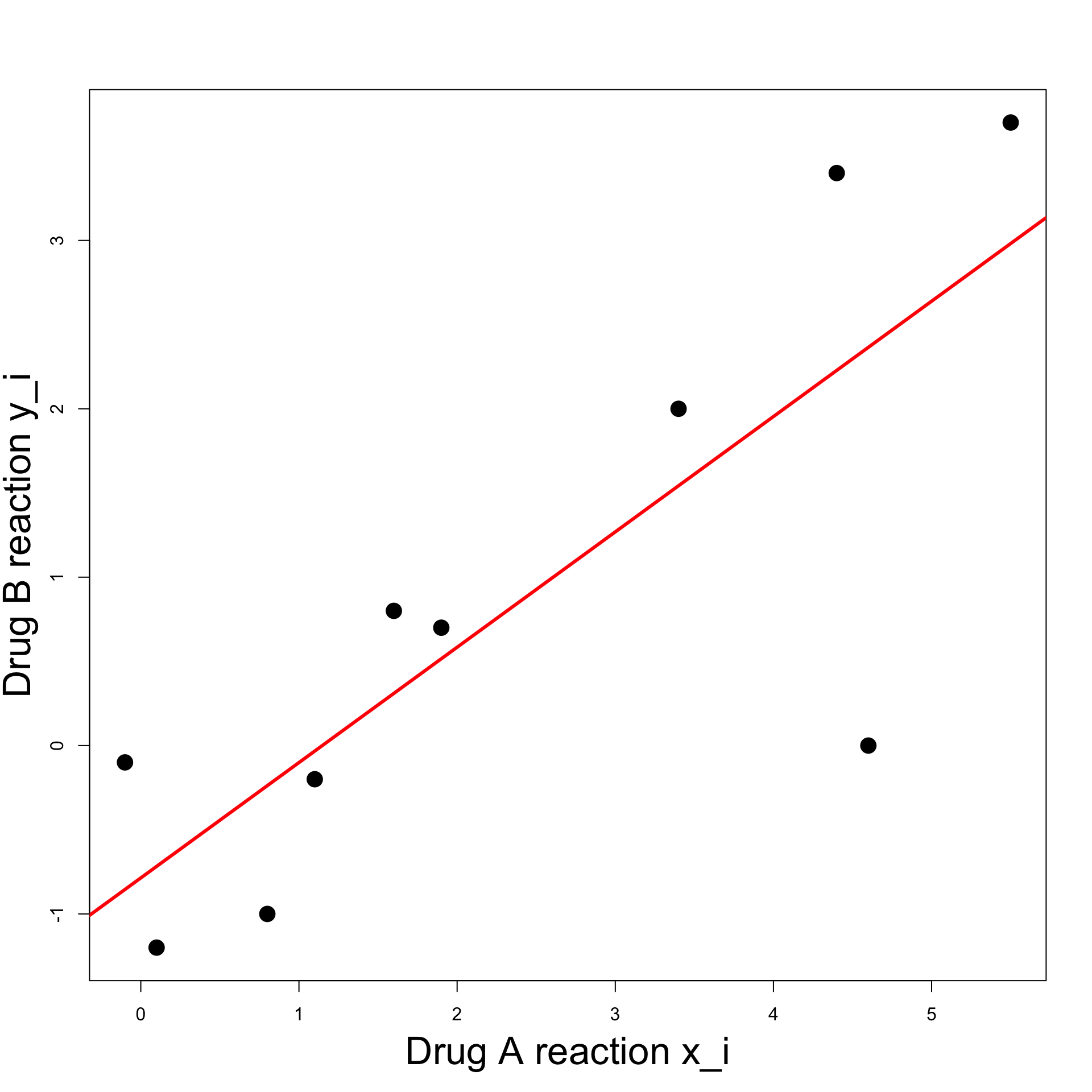
  • Plot the data pairs (x_i,y_i)
# Plot the data
plot(x, y, xlab = "", ylab = "", pch = 16, cex = 2)

# Add labels
mtext("Drug A reaction x_i", side = 1, line = 3, cex = 2.1)
mtext("Drug B reaction y_i", side = 2, line = 2.5, cex = 2.1)
  • Note: We have added a few cosmetic options
    • pch = 16 plots points with black circles
    • cex = 2 stands for character expansion – Specifies width of points
    • xlab = "" and ylab = "" add empty axis labels

Exercise: Blood Pressure

First Solution

  • Plot the data pairs (x_i,y_i)
# Plot the data
plot(x, y, xlab = "", ylab = "", pch = 16, cex = 2)

# Add labels
mtext("Drug A reaction x_i", side = 1, line = 3, cex = 2.1)
mtext("Drug B reaction y_i", side = 2, line = 2.5, cex = 2.1)
  • Note: We have added a few cosmetic options
    • mtext is used to fine-tune the axis labels
    • side = 1 stands for x-axis
    • side = 2 stands for y-axis
    • line specifies distance of label from axis

Exercise: Blood Pressure

First Solution

  • To plot the least-squares line we need to
    • Create grid of x coordinates and compute y = \hat \beta x + \hat \alpha over such grid
    • Plot the pairs (x,y) and interpolate
# Compute least-squares line on grid
x_grid <- seq(from = -1, to = 6, by = 0.1)
y_grid <- beta * x_grid + alpha

# Plot the least-squares line
lines(x_grid, y_grid, col = "red", lwd = 3)
  • Note: Cosmetic options
    • col specifies color of the plot
    • lwd specifies line width

Exercise: Blood Pressure

First Solution

  • Previous code can be downloaded here least_squares_1.R

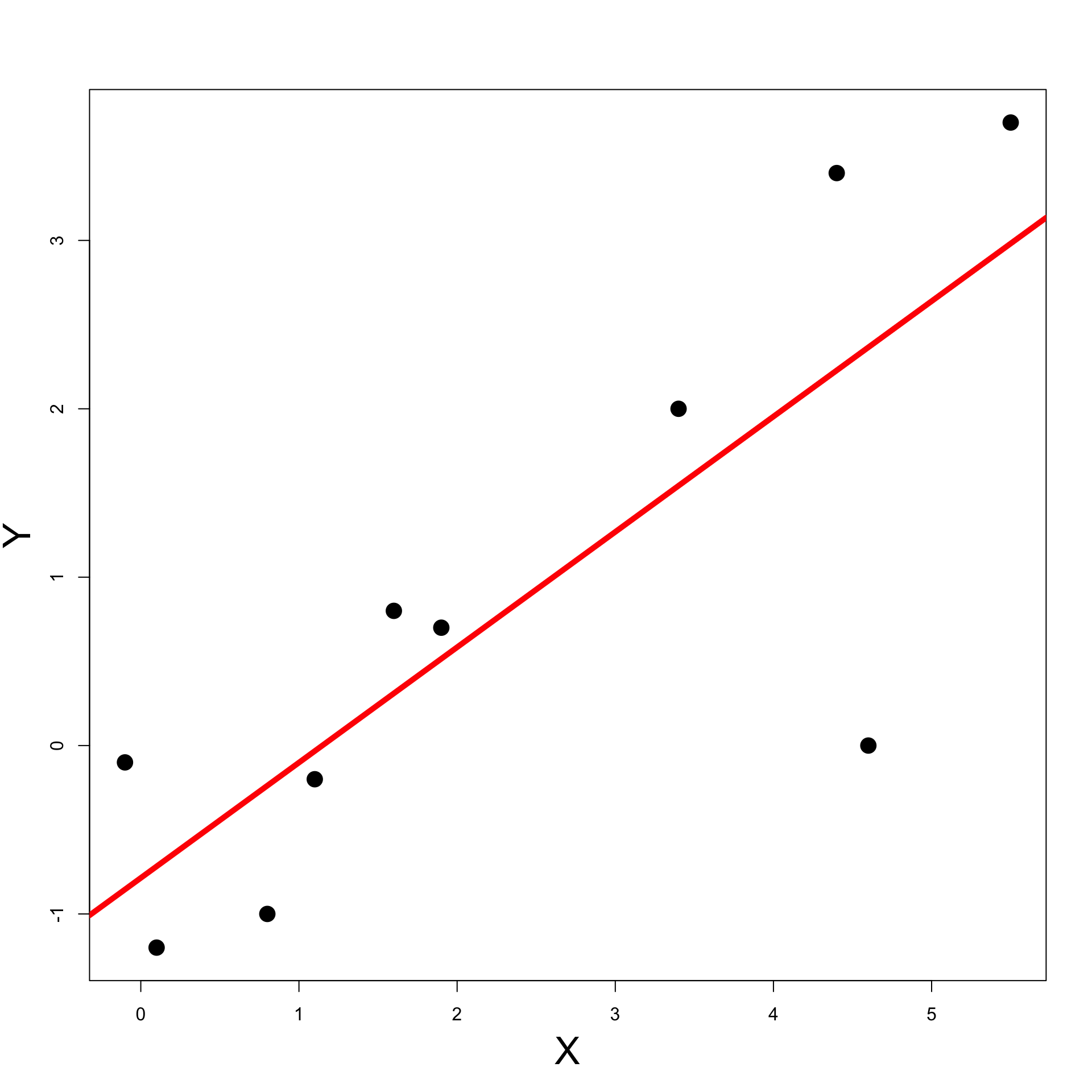
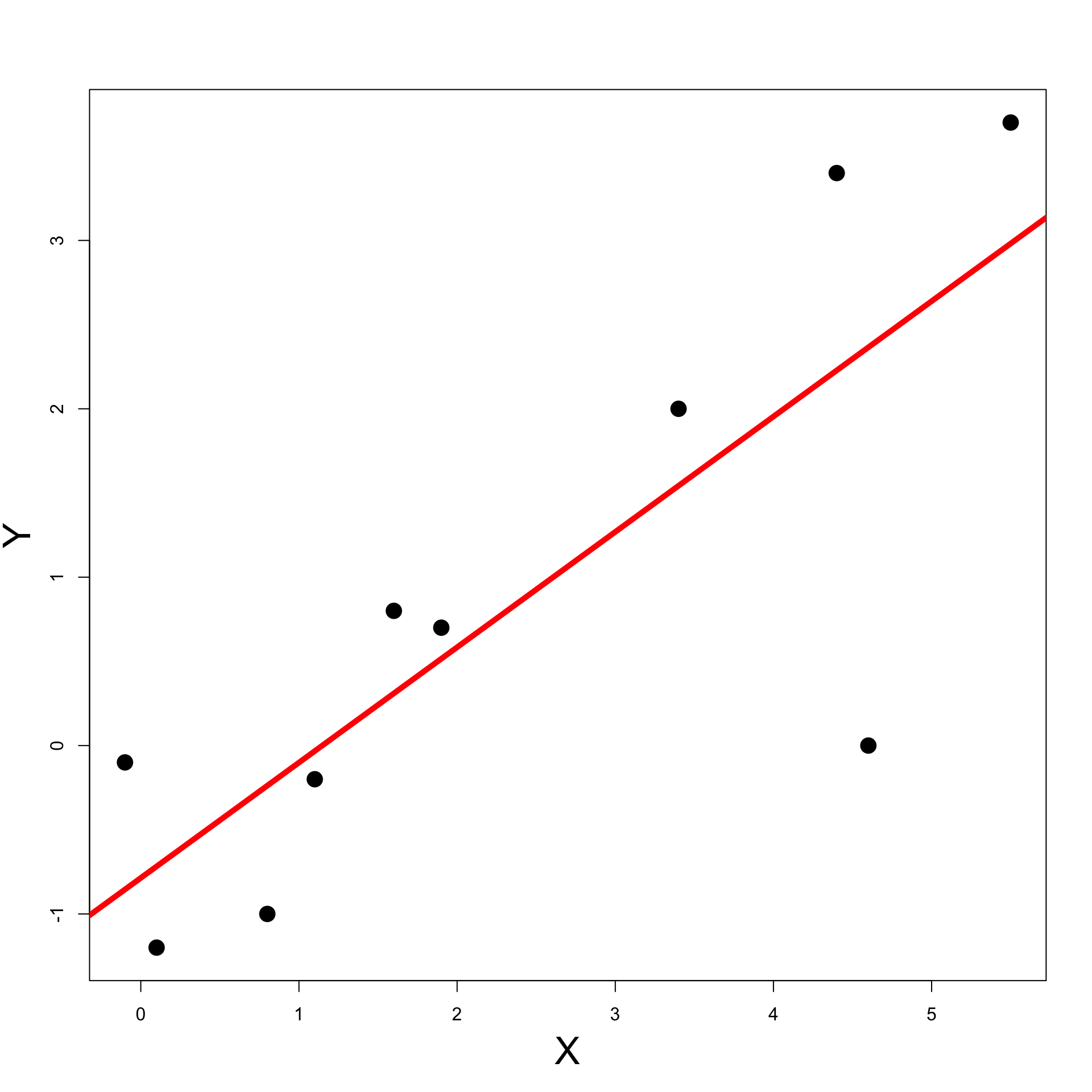
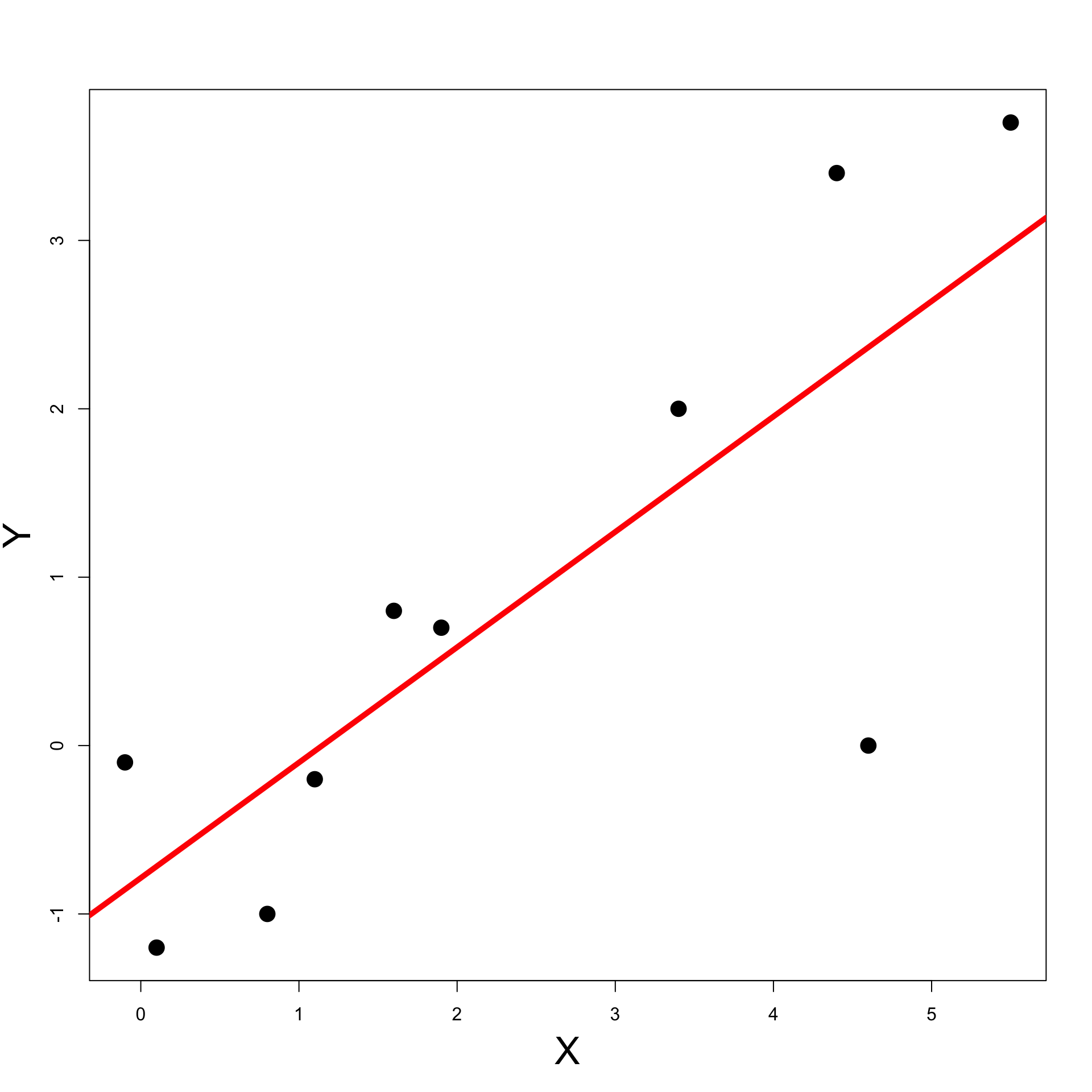
  • Running the code we obtain the plot on the right

Exercise: Blood Pressure

Second Solution

  • The second solution uses the R function lm
  • lm stands for linear model
  • First we input the data into a data-frame
# Input blood pressure changes data into data-frame
changes <- data.frame(drug_A = c(1.9, 0.8, 1.1, 0.1, -0.1, 
                                 4.4, 4.6, 1.6, 5.5, 3.4),
                      drug_B = c(0.7, -1.0, -0.2, -1.2, -0.1, 
                                 3.4, 0.0, 0.8, 3.7, 2.0)
                     )

Exercise: Blood Pressure

Second Solution

  • We now use lm to fit the least-squares line

  • The basic syntax of lm is

    • lm(formula, data)
    • data expects a data-frame in input
    • formula stands for the relation to fit

  • In case of least-squares the formula is

    • formula = y ~ x

  • The symbol y ~ x can be read as

    • y modelled as function of x

  • x and y are the names of two variables in the data-frame

Exercise: Blood Pressure

Second Solution

  • Storing data in data-frame is optional
    • We can instead use vectors x and y
  • We can fit the least-squares line with command
    • lm(y ~ x)

Exercise: Blood Pressure

Second Solution

  • The command to fit the least-squares line on changes is
least_squares <- lm(formula = drug_B ~ drug_A, data = changes)
  • This is what R plots when calling print(least_squares)

Call:
lm(formula = drug_B ~ drug_A, data = changes)

Coefficients:
(Intercept)       drug_A  
    -0.7861       0.6850
  • The above tells us that the estimators are

\hat \alpha = -0.7861 \,, \qquad \quad \hat \beta = 0.6850

Exercise: Blood Pressure

Second Solution

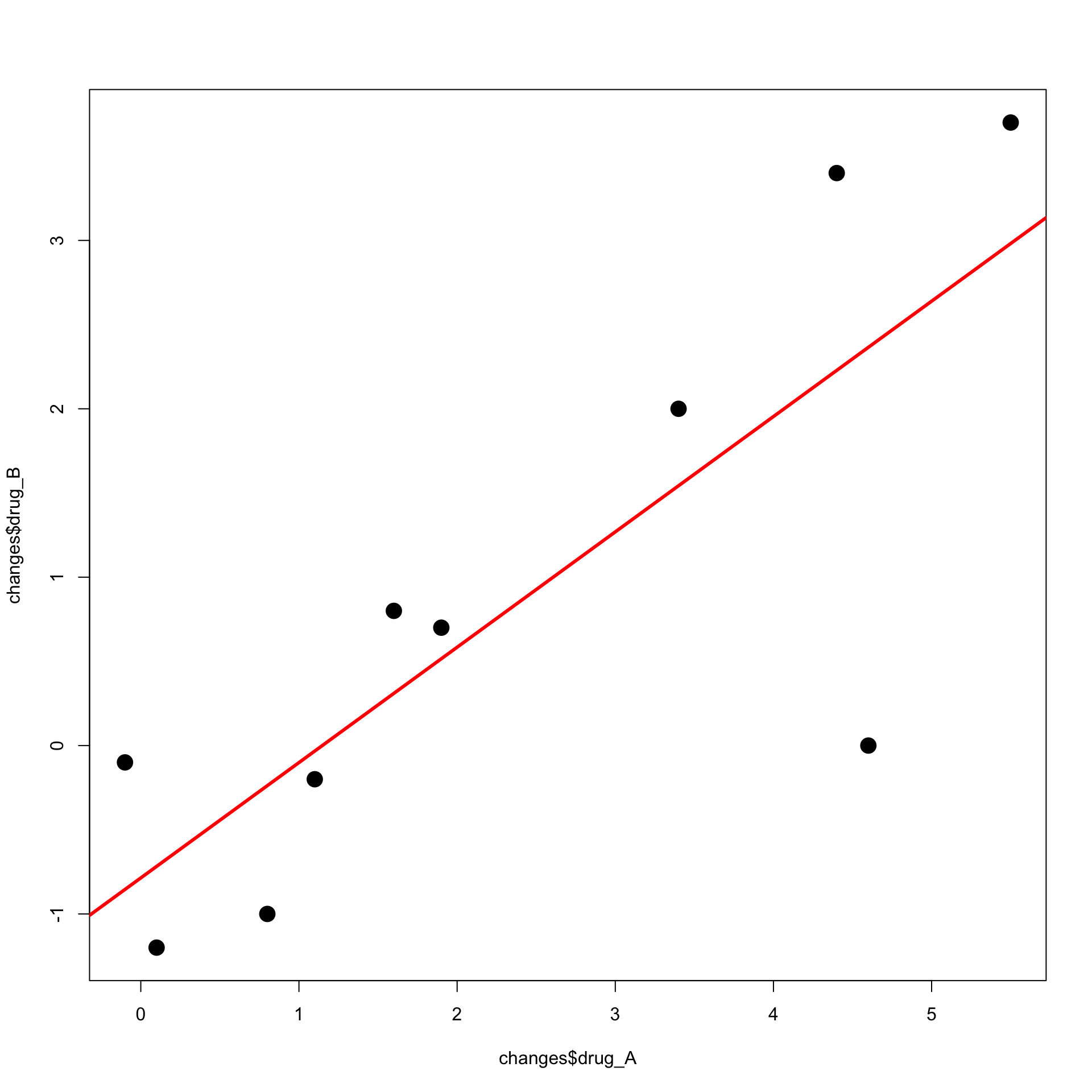
  • We can now plot the data with the following command
    • 1st coordinate is the vector changes$drug_A
    • 2nd coordinate is the vector changes$drug_B
# Plot data 
plot(changes$drug_A, changes$drug_B, pch = 16, cex = 2)

  • The least-squares line is currently stored in least_squares

  • To add such line to the current plot use abline

# Plot least-squares line
abline(least_squares, col = "red", lwd = 3)

Exercise: Blood Pressure

Second Solution

  • Previous code can be downloaded here least_squares_2.R

  • Running the code we obtain the plot on the right

Part 2:
Simple linear
regression

Simple linear regression

Motivation

  • Model: Suppose to have two random variables X and Y
    • X models observed values
    • Y models a response
  • Goal of Regression: Learn the distribution of Y | X
    • Y | X allows to predict values of Y from values of X

Simple linear regression

Motivation

  • Note: To learn Y|X one would need joint distribution of (X,Y)

  • Problem: The joint distribution of (X,Y) is unknown

  • Data: We have partial knowledge on (X,Y) in the form of

    • paired observations (x_1,y_1) , \ldots, (x_n,y_n)
    • (x_i,y_i) is observed from (X,Y)

  • Goal:Use the data to learn Y|X

Simple linear regression

Motivation

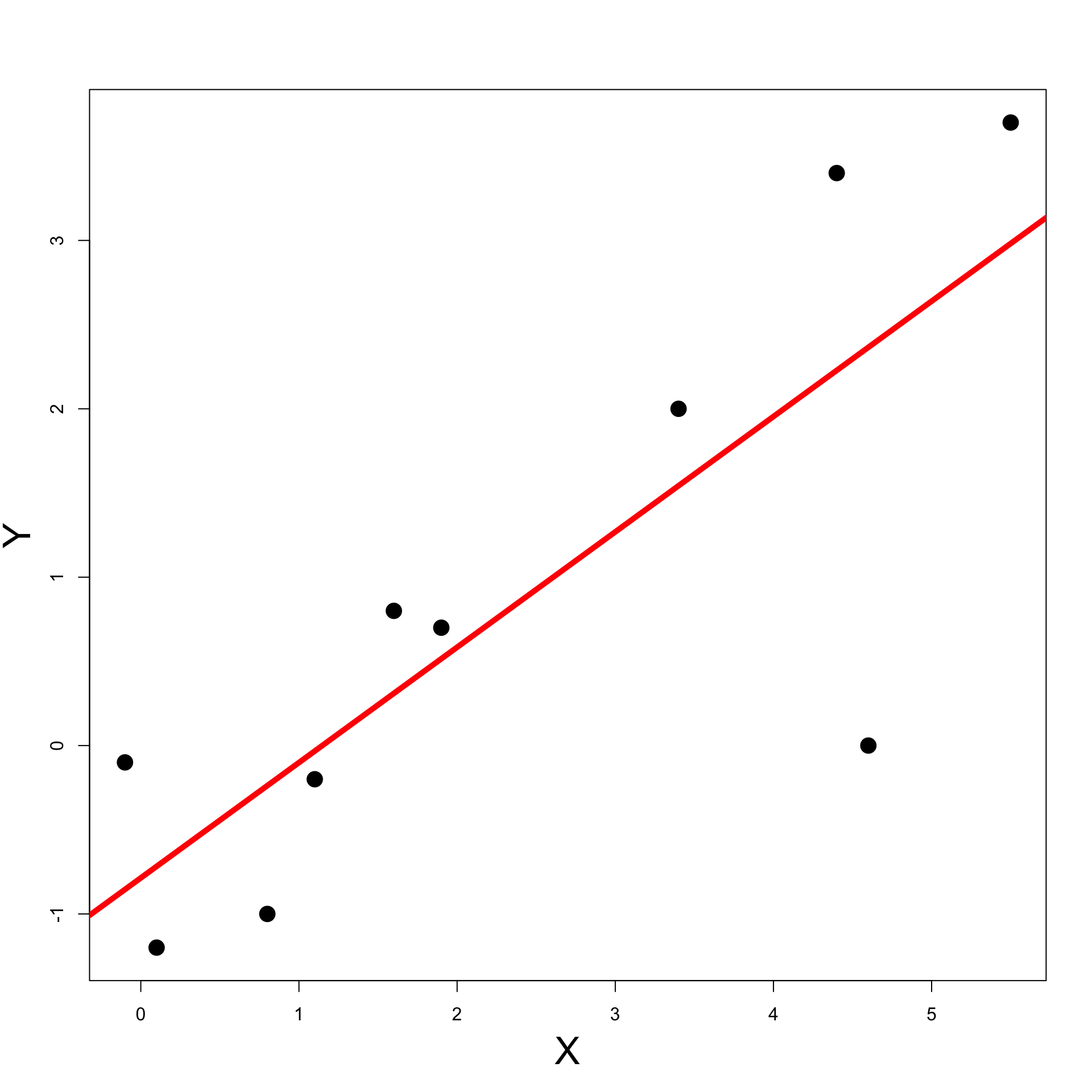
Least-Squares:

  • Naive solution to regression problem

  • Find a line of best fit y = \hat \alpha + \hat \beta x

  • Such line explains the data, i.e., y_i \ \approx \ \hat \alpha + \hat \beta x_i

Simple linear regression

Motivation

Drawbacks of least squares:

  • Only predicts values of y such that (x,y) \, \in \, \text{ Line}

  • Ignores that (x_i,y_i) comes from joint distribution (X,Y)

Simple linear regression

Motivation

Linear Regression:

  • Find a regression line R(x) = \alpha + \beta x

  • R(x) predicts most likely value of Y when X = x

Simple linear regression

Motivation

Linear Regression:

  • We will see that regression line coincides with line of best fit R(x) = \hat \alpha + \hat \beta x

  • Hence regression gives statistical meaning to the line of best fit

Regression function

Definition

Suppose given two random variables X and Y

  • X is the predictor
  • Y is the response

Definition
The regression function of Y on X is the conditional expectation

R \colon \mathbb{R}\to \mathbb{R}\,, \qquad \quad R(x) := {\rm I\kern-.3em E}[Y | X = x]

Regression function

Interpretation

Idea
The regression function R(x) = {\rm I\kern-.3em E}[Y | X = x] predicts the most likely value of Y when we observe X = x

Notation: We use the shorthand {\rm I\kern-.3em E}[Y|x] := {\rm I\kern-.3em E}[Y | X = x]

The regression problem

Assumption: Suppose to have n observations (x_1,y_1) \,, \ldots , (x_n, y_n)

  • x_i observed from X
  • y_i observed from Y

Problem
From (x_1,y_1) \,, \ldots , (x_n, y_n) learn a regression function {\rm I\kern-.3em E}[Y | x] which explains the observations, that is, {\rm I\kern-.3em E}[Y | x_i] \ \approx \ y_i \,, \qquad \forall \, i = 1 , \ldots, n

Simple linear regression

  • Regression problem is difficult without prior knowledge on {\rm I\kern-.3em E}[Y | x]

  • A popular model is to assume that {\rm I\kern-.3em E}[Y | x] is linear

Definition
The regression function of Y on X is linear if there exist \alpha and \beta s.t. {\rm I\kern-.3em E}[Y | x] = \alpha + \beta x \,, \qquad \forall \, x \in \mathbb{R}

  • \alpha and \beta are called regression coefficients

  • The above regression is called simple because only 2 variables are involved

What do we mean by linear?

Note: We said that the regression is linear if {\rm I\kern-.3em E}[Y | x ] = \alpha + \beta x In the above we mean linearity wrt the parameters \alpha and \beta

Examples:

  • Linear regression of Y on X^2 is {\rm I\kern-.3em E}[Y | x^2 ] = \alpha + \beta x^2

  • Linear regression of \log Y on 1/X is {\rm I\kern-.3em E}[ \log Y | x ] = \alpha + \beta \frac{1}{ x }

Simple linear regression

Model Assumptions

Suppose to have n observations (x_1,y_1) \,, \ldots , (x_n, y_n)

  • x_i observed from X
  • y_i observed from Y

Definition
For each i = 1 , \ldots, n we denote by Y_i a random variable with distribution Y | X = x_i

Assumptions:

  1. Predictor is known: The values x_1, \ldots, x_n are known

Simple linear regression

Model Assumptions

  1. Normality: The distribution of Y_i is normal

  2. Linear mean: There are parameters \alpha and \beta such that {\rm I\kern-.3em E}[Y_i] = \alpha + \beta x_i

  3. Common variance (Homoscedasticity): There is a parameter \sigma^2 such that {\rm Var}[Y_i] = \sigma^2

  4. Independence: The random variables Y_1 \,, \ldots \,, Y_n are independent

Characterization of the Model

  • Assumptions 1–5 look quite abstract
  • The following Proposition gives a handy characterization

Proposition
Assumptions 1-5 are satisfied if and only if Y_i = \alpha + \beta x_i + \varepsilon_i for some random variables \varepsilon_1 , \ldots, \varepsilon_n \,\, \text{ iid } \,\, N(0,\sigma^2)

  • The terms \varepsilon_i are called errors

Characterization of the Model

Proof

  • By Assumption 2 we have that Y_i is normal

  • By Assumption 3 and 4 we have

{\rm I\kern-.3em E}[Y_i] = \alpha + \beta x_i \,, \qquad \quad {\rm Var}[Y_i] = \sigma^2

  • Therefore

Y_i \sim N(\alpha + \beta x_i, \sigma^2)

Characterization of the Model

Proof

  • Define the random variables

\varepsilon_i := Y_i - (\alpha + \beta x_i)

  • By Assumption 5 we have that Y_1,\ldots,Y_n are independent

  • Therefore \varepsilon_1,\ldots,\varepsilon_n are independent

  • Since Y_i \sim N(\alpha + \beta x_i, \sigma^2) we conclude that

\varepsilon_i \sim N(0,\sigma^2)

Likelihood function

Definition
Let X_1, \ldots, X_n be continuous rv with joint pdf f = f(x_1, \ldots, x_n | \theta) depending on a parameter \theta \in \Theta. The likelihood function of the random vector (X_1, \ldots, X_n) for a given sample (x_1, \ldots, x_n) is L \colon \Theta \to \mathbb{R}\,, \qquad \quad L(\theta | x_1,\ldots, x_n ) := f(x_1, \ldots, x_n | \theta)

Likelihood function

Proposition
Suppose Assumptions 1–5 hold. The likelihood function of linear regression is L(\alpha,\beta, \sigma^2 | y_1, \ldots, y_n ) = \frac{1}{(2\pi \sigma^2)^{n/2}} \, \exp \left( -\frac{\sum_{i=1}^n(y_i-\alpha - \beta x_i)^2}{2\sigma^2} \right)

Likelihood function

Proof

  • Recall that

Y_i \sim N( \alpha + \beta x_i , \sigma^2 )

  • Therefore the pdf of Y_i is

f_{Y_i} (y_i) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp \left( -\frac{(y_i-\alpha-\beta{x_i})^2}{2\sigma^2} \right)

Likelihood function

Proof

  • Since Y_1,\ldots, Y_n are independent we obtain \begin{align*} L(\alpha,\beta, \sigma^2 | y_1, \ldots,y_n) & = f(y_1,\ldots,y_n) \\ & = \prod_{i=1}^n f_{Y_i}(y_i) \\ & = \prod_{i=1}^n \frac{1}{\sqrt{2\pi \sigma^2}} \exp \left( -\frac{(y_i-\alpha-\beta{x_i})^2}{2\sigma^2} \right) \\ & = \frac{1}{(2\pi \sigma^2)^{n/2}} \, \exp \left( -\frac{\sum_{i=1}^n(y_i- \alpha - \beta x_i)^2}{2\sigma^2} \right) \end{align*}

Model Summary

  • Simple linear regression of Y on X is the function

{\rm I\kern-.3em E}[Y | x] = \alpha + \beta x

  • Suppose given the observations from (X,Y)

(x_1,y_1) , \ldots , (x_n, y_n)

Model Summary

  • Denote by Y_i the random variable

Y | X = x_i

  • We suppose that Y_i has the form

Y_i = \alpha + \beta x_i + \varepsilon_i

  • The errors \varepsilon_1,\ldots, \varepsilon_n are iid N(0,\sigma^2)

The linear regression problem

Problem
From (x_1,y_1) \,, \ldots , (x_n, y_n) learn a linear regression function {\rm I\kern-.3em E}[Y | x] = \alpha + \beta x which explains the observations, that is, \begin{equation} \tag{3} {\rm I\kern-.3em E}[Y | x_i] \ \approx \ y_i \,, \qquad \forall \, i = 1 , \ldots, n \end{equation}

Question
How do we enforce (3)?

Answer

  • Recall that Y_i is distributed like

Y | x_i

  • Therefore

{\rm I\kern-.3em E}[Y | x_i] = {\rm I\kern-.3em E}[Y_i]

  • Hence (3) holds iff

\begin{equation} \tag{4} {\rm I\kern-.3em E}[Y_i] \ \approx \ y_i \,, \qquad \forall \, i = 1 , \ldots, n \end{equation}

Answer

  • If we want (4) to hold, we need to maximize the joint probability

P(Y_1 \approx y_1, \ldots, Y_n \approx y_n)

  • This means choosing parameters \hat \alpha, \hat \beta, \hat \sigma which maximize the likelihood function

\max_{\alpha,\beta,\sigma} \ L(\alpha,\beta, \sigma^2 | y_1, \ldots, y_n )

Maximizing the likelihood

Theorem
Suppose Assumptions 1–5 hold and assume given n observations (x_1,y_1), \ldots, (x_n,y_n). The maximization problem \max_{\alpha,\beta,\sigma} \ L(\alpha,\beta, \sigma^2 | y_1, \ldots, y_n ) admits the unique solution \hat \alpha = \overline{y} - \hat \beta \, \overline{x} \,, \qquad \hat \beta = \frac{S_{xy}}{S_{xy}} \,, \qquad \hat{\sigma}^2 = \frac{1}{n} \sum_{i=1}^n \left( y_i - \hat \alpha - \hat \beta x_i \right)^2

Note: The coefficients \hat \alpha and \hat \beta are the same of least-squares line!

Maximizing the likelihood

Proof of Theorem

  • The \log function is strictly increasing

  • Therefore the problem \max_{\alpha,\beta,\sigma} \ L(\alpha,\beta, \sigma^2 | y_1, \ldots, y_n ) is equivalent to \max_{\alpha,\beta,\sigma} \ \log L( \alpha,\beta, \sigma^2 | y_1, \ldots, y_n )

Maximizing the likelihood

Proof of Theorem

  • Recall that the likelihood is L(\alpha,\beta, \sigma^2 | y_1, \ldots, y_n ) = \frac{1}{(2\pi \sigma^2)^{n/2}} \, \exp \left( - \frac{\sum_{i=1}^n(y_i-\alpha - \beta x_i)^2}{2\sigma^2} \right)

  • Hence the log–likelihood is \log L(\alpha,\beta, \sigma^2 | y_1, \ldots, y_n ) = - \frac{n}{2} \log (2 \pi) - \frac{n}{2} \log \sigma^2 - \frac{ \sum_{i=1}^n(y_i-\alpha - \beta x_i)^2 }{2 \sigma^2}

Maximizing the likelihood

Proof of Theorem

Suppose \sigma is fixed. In this case the problem \max_{\alpha,\beta} \ \left\{ \frac{n}{2} \log (2 \pi) - \frac{n}{2} \log \sigma^2 - \frac{ \sum_{i=1}^n(y_i-\alpha - \beta x_i)^2 }{2 \sigma^2} \right\} is equivalent to \min_{\alpha, \beta} \ \sum_{i=1}^n(y_i-\alpha - \beta x_i)^2

This is the least-squares problem! Hence the solution is \hat \alpha = \overline{y} - \hat \beta \, \overline{x} \,, \qquad \hat \beta = \frac{S_{xy}}{S_{xy}}

Maximizing the likelihood

Proof of Theorem

  • Substituting \hat \alpha and \hat \beta we obtain \begin{align*} \max_{\alpha,\beta,\sigma} \ & \log L(\alpha,\beta, \sigma^2 | y_1, \ldots, y_n ) = \max_{\sigma} \ \log L(\hat \alpha, \hat \beta, \sigma^2 | y_1, \ldots, y_n ) \\[10pt] & = \max_{\sigma} \ \left\{ - \frac{n}{2} \log (2 \pi) - \frac{n}{2} \log \sigma^2 - \frac{ \sum_{i=1}^n(y_i-\hat\alpha - \hat\beta x_i)^2 }{2 \sigma^2} \right\} \end{align*}

  • It can be shown that the unique solution to the above problem is \hat{\sigma}^2 = \frac{1}{n} \sum_{i=1}^n \left( y_i - \hat \alpha - \hat \beta x_i \right)^2

  • This concludes the proof

Least-squares vs Linear regression

Linear regression and least-squares give seemingly the same answer

Least-squares line y = \hat \alpha + \hat \beta x
Linear regression line {\rm I\kern-.3em E}[Y | x ] = \hat \alpha + \hat \beta x

Question: Why did we define regression if it gives same answer as least-squares?

Least-squares vs Linear regression

Answer: There is actually a big difference

  • Least-squares line y = \hat \alpha + \hat \beta x
    • Just a geometric object
    • Can only predict pairs (x,y) which lie on the line
    • Ignores statistical nature of the problem
  • Regression line {\rm I\kern-.3em E}[Y | x ] = \hat \alpha + \hat \beta x
    • Statistical model for Y|X via the estimation of {\rm I\kern-.3em E}[Y | x]
    • Can predict most likely values of Y given the observation X = x
    • Can test how well the linear model fits the data

References

Homepage      License      Contact

[1]
Fusco, Nicola, Marcellini, Paolo, Sbordone, Carlo, Mathematical analysis: Functions of several real variables and applications, Springer, 2022.