Statistical Models

Lecture 3

Dr. Silvio Fanzon

S.Fanzon@hull.ac.uk

University of Hull

Dr. John Fry

J.M.Fry@hull.ac.uk

University of Hull

Lecture 3:
Random samples

Outline of Lecture 3

1. Random samples
2. Unbiased estimators
3. Chi squared distribution
4. Sampling from normal distribution
5. t-distribution
6. Hypothesis testing

Part 1:
Random samples

Independent identically distributed random variables

Definition

The random variables X_1,\ldots,X_n are independent identically distributed or iid with pdf or pmf f(x) if

• X_1,\ldots,X_n are mutually independent
• The marginal pdf or pmf of each X_i satisfies f_{X_i}(x) = f(x) \,, \quad \forall \, x \in \mathbb{R}

Random sample

• Suppose the data in an experiment consists of observations on a population
• Suppose the population has distribution f(x)
• Each observation is labelled X_i
• We always assume that the population is infinite
• Therefore each X_i has distribution f(x)
• We also assume the observations are independent

Definition

The random variables X_1,\ldots,X_n are a random sample of size n from the population f(x) if X_1,\ldots,X_n are iid with pdf or pmf f(x)

Random sample

Remark: Let X_1,\ldots,X_n be a random sample of size n from the population f(x). Then the joint distribution of \mathbf{X}= (X_1,\ldots,X_n) is f_{\mathbf{X}}(x_1,\ldots,x_n) = f(x_1) \cdot \ldots \cdot f(x_n) = \prod_{i=1}^n f(x_i)

Definition

We call f_{\mathbf{X}} the joint sample distribution

Random sample

Notation:

• When the population distribution f(x) depends on a parameter \theta we write f = f(x|\theta)

• In this case the joint sample distribution is f_{\mathbf{X}}(x_1,\ldots,x_n | \theta) = \prod_{i=1}^n f(x_i | \theta)

Example

• Suppose a population has \mathop{\mathrm{Exponential}}(\beta) distribution f(x|\beta) = \frac{1}{\beta} e^{-x/\beta}
• Suppose X_1,\ldots,X_n is random sample from the population f(x|\beta)
• The joint sample distribution is then \begin{align*} f_{\mathbf{X}}(x_1,\ldots,x_n | \beta) & = \prod_{i=1}^n f(x_i|\beta) \\ & = \prod_{i=1}^n \frac{1}{\beta} e^{-x_i/\beta} \\ & = \frac{1}{\beta^n} e^{-(x_1 + \ldots + x_n)/\beta} \end{align*}

Example

• We have P(X_1 > 2) = \int_{2}^\infty f(x|\beta) \, dx = \int_{2}^\infty \frac{1}{\beta} e^{-x/\beta} \, dx = e^{-2/\beta}

• Thanks to iid assumption we can easily compute \begin{align*} P(X_1 > 2 , \ldots, X_n > 2) & = \prod_{i=1}^n P(X_i > 2) \\ & = \prod_{i=1}^n P(X_1 > 2) \\ & = P(X_1 > 2)^n \\ & = e^{-2n/\beta} \end{align*}

Part 2:
Unbiased estimators

Point estimation

Suppose to have a population with distribution f(x|\theta)

• \theta is generally unknown
• Knowledge of \theta is sufficient to characterize f(x|\theta)

Example: A population could be normally distributed f(x|\mu,\sigma^2)

• Here \mu is the mean and \sigma^2 the variance
• Knowing \mu and \sigma^2 completely characterizes the normal distribution

Point estimation

Definition

Suppose the population has distribution f(x|\theta)

• Point estimation is the procedure of estimating \theta from random sample
• A point estimator is any function of a random sample W(X_1,\ldots,X_n)

Notation: Point estimators are also called statistics

Unbiased estimator

Definition

Suppose W is a point estimator of a parameter \theta

• The bias of W is the quantity \rm{Bias}_{\theta} := {\rm I\kern-.3em E}[W] - \theta

• W is an unbiased estimator if \rm{Bias}_{\theta} = 0, that is, {\rm I\kern-.3em E}[W] = \theta

Note: A point estimator W = W(X_1, \ldots, X_n) is itself a random variable. Thus {\rm I\kern-.3em E}[W] is the mean of such random variable

Examples

We give two examples of unbiased estimators:

• Sample mean
• Sample variance

Estimating the mean

Problem

Suppose to have a population f(x|\theta) We want to estimate the population mean \mu := \int_{\mathbb{R}} x f(x|\theta) \, dx

Sample mean

Definition

The sample mean of a random sample X_1,\ldots,X_n is the statistic W(X_1,\ldots,X_n) := \overline{X} := \frac{1}{n} \sum_{i=1}^n X_i

Sample mean

Sample mean is unbiased estimator of mean

Theorem

The sample mean \overline{X} is an unbiased estimator of the population mean \mu, that is, {\rm I\kern-.3em E}[\overline{X}] = \mu

Sample mean

Proof of theorem

• X_1,\ldots,X_n is a random sample from f(x|\theta)
• Therefore X_i \sim f(x|\theta) and {\rm I\kern-.3em E}[X_i] = \int_{\mathbb{R}} x f(x|\theta) \, dx = \mu
• By linearity of expectation we have {\rm I\kern-.3em E}[\overline{X}] = \frac{1}{n} \sum_{i=1}^n {\rm I\kern-.3em E}[X_i] = \frac{1}{n} \sum_{i=1}^n \mu = \mu

Sample mean

Computing the variance

It is useful to compute the variance of the sample mean \overline{X}

Lemma

X_1,\ldots,X_n random sample from population with mean \mu and variance \sigma^2. Then {\rm Var}[\overline{X}] = \frac{\sigma^2}{n}

Sample mean

Proof of Lemma

• By assumption we have {\rm I\kern-.3em E}[X_i] = \mu \,, \quad {\rm Var}[X_i] = \sigma^2

• Since the variance is quadratic and X_i are independent \begin{align*} {\rm Var}[\overline{X}] & = {\rm Var}\left[ \frac{1}{n} \sum_{i=1}^n X_i \right] = \frac{1}{n^2} \sum_{i=1}^n {\rm Var}[X_i] \\ & = \frac{1}{n^2} \cdot n \sigma^2 = \frac{\sigma^2}{n} \end{align*}

Estimating the variance

Problem

Suppose to have a population f(x|\theta) with mean \mu and variance \sigma^2. We want to estimate the population variance

Sample variance

Definition

The sample variance of a random sample X_1,\ldots,X_n is the statistic S^2 := \frac{1}{n-1} \sum_{i=1}^n \left( X_i - \overline{X} \right)^2 where \overline{X} is the sample mean \overline{X} := \frac{1}{n} \sum_{i=1}^n X_i

Sample variance

Equivalent formulation

Proposition

It holds that S^2 := \frac{ \sum_{i=1}^n \left( X_i - \overline{X} \right)^2}{n-1} = \frac{ \sum_{i=1}^n X_i^2 - n\overline{X}^2 }{n-1}

Sample variance

Proof of Proposition

• We have \begin{align*} \sum_{i=1}^n \left( X_i - \overline{X} \right)^2 & = \sum_{i=1}^n \left(X_i^2 + \overline{X}^2 - 2 X_i \overline{X} \right) = \sum_{i=1}^n X_i^2 + n\overline{X}^2 - 2 \overline{X} \sum_{i=1}^n X_i \\ & = \sum_{i=1}^n X_i^2 + n\overline{X}^2 - 2 n \overline{X}^2 = \sum_{i=1}^n X_i^2 -n \overline{X}^2 \end{align*}

• Dividing by n-1 yields the desired identity S^2 = \frac{ \sum_{i=1}^n X_i^2 -n \overline{X}^2 }{n-1}

Sample variance

Sample variance is unbiased estimator of variance

Theorem

The sample variance S^2 is an unbiased estimator of the population variance \sigma^2, that is, {\rm I\kern-.3em E}[S^2] = \sigma^2

Sample variance

Proof of theorem

• X_1,\ldots,X_n is a random sample from f(x|\theta)

• By linearity of expectation we infer \begin{align*} {\rm I\kern-.3em E}[(n-1)S^2] & = {\rm I\kern-.3em E}\left[ \sum_{i=1}^n X_i^2 - n\overline{X}^2 \right] \\ & = \sum_{i=1}^n {\rm I\kern-.3em E}[X_i^2] - n {\rm I\kern-.3em E}[\overline{X}^2] \end{align*}

Sample variance

Proof of theorem

• Since X_i \sim f(x|\theta), we have {\rm I\kern-.3em E}[X_i] = \mu \,, \quad {\rm Var}[X_i] = \sigma^2

• Therefore by definition of variance we get {\rm I\kern-.3em E}[X_i^2] = {\rm Var}[X_i] + {\rm I\kern-.3em E}[X]^2 = \sigma^2 + \mu^2

Sample variance

Proof of theorem

• Also recall that {\rm I\kern-.3em E}[\overline{X}] = \mu \,, \quad {\rm Var}[\overline{X}] = \frac{\sigma^2}{n}

• By definition of variance we get {\rm I\kern-.3em E}[\overline{X}^2] = {\rm Var}[\overline{X}] + {\rm I\kern-.3em E}[\overline{X}]^2 = \frac{\sigma^2}{n} + \mu^2

Sample variance

Proof of theorem

• Hence \begin{align*} {\rm I\kern-.3em E}[(n-1)S^2] & = \sum_{i=1}^n {\rm I\kern-.3em E}[X_i^2] - n {\rm I\kern-.3em E}[\overline{X}^2] \\ & = \sum_{i=1}^n \left( \mu^2 + \sigma^2 \right) - n \left( \mu^2 + \frac{\sigma^2}{n} \right) \\ & = n\mu^2 + n\sigma^2 - n \mu^2 - \sigma^2 \\ & = (n-1) \sigma^2 \end{align*}

• Dividing both sides by (n-1) yields the thesis {\rm I\kern-.3em E}[S^2] = \sigma^2

Notation

• The realization of a random sample X_1,\ldots,X_n is denoted by x_1, \ldots, x_n

• The realization of the sample mean \overline{X} is denoted \overline{x} := \frac{1}{n} \sum_{i=1}^n x_i

• The realization of the sample variance S^2 is denoted s^2=\frac{\sum_{i=1}{n}(x_i-\overline{x})^2}{n-1}=\frac{\sum_{i=1}^n x_i^2-n{\overline{x}^2}}{n-1}

Additional note

• The n-1 factor in the denominator of the sample variance estimator s^2=\frac{\sum_{i=1}{n}(x_i-\overline{x})^2}{n-1}=\frac{\sum_{i=1}^n x_i^2-n{\overline{x}^2}}{n-1} is caused by a loss of precision:

  • We have to estimate \mu with the sample mean \overline{x}

• This leads to a general statistical rule: \text{Lose 1 degree of freedom for each parameter estimated}

• In this we have to estimate one parameter (the sample mean ). Hence \begin{align*} \text{degrees of freedom} & = \text{Sample size}-\text{No. of estimated parameters} \\ & = n-1 \end{align*}

Example calculation

• Wage data on 10 Advertising Professionals Accountants

Professional	x_1	x_2	x_3	x_4	x_5	x_6	x_7	x_8	x_9	x_{10}
Wage	36	40	46	54	57	58	59	60	62	63

• Task: Estimate population mean and variance

Solution to the example

• Number of advertising professionals n=10

• Sample Mean: \overline{x} = \frac{1}{n} \sum_{i=1}^n x_i = \frac{36+40+46+{\dots}+62+63}{10}=\frac{535}{10}=53.5

• Sample Variance: \begin{align*} s^2 & = \frac{\sum_{i=1}^n x_{i}^2 - n \overline{x}^2}{n-1} \\ \sum_{i=1}^n x_i^2 & = 36^2+40^2+46^2+{\ldots}+62^2+63^2 = 29435 \\ s^2 & = \frac{29435-10(53.5)^2}{9} = 90.2778 \end{align*}

Part 3:
Chi squared distribution

Overview

Chi-squared distribution:

• defined in terms of squares of N(0, 1) random variables
• designed to describe variance estimation
• used to define other members of the normal family
  • Student t-distribution
  • F-distribution

Why the normal family is important

• Classical hypothesis testing and regression problems
• The same maths solves apparently unrelated problems
• Easy to compute
  • Statistics tables
  • Software
• Enables the development of approximate methods in more complex (and interesting) problems

Reminder: Normal distribution

• X has normal distribution with mean \mu and variance \sigma^2 if pdf is f(x) := \frac{1}{\sqrt{2\pi\sigma^2}} \, \exp\left( -\frac{(x-\mu)^2}{2\sigma^2}\right) \,, \quad x \in \mathbb{R}

• In this case we write X \sim N(\mu,\sigma^2)

• The standard normal distribution is denoted N(0,1)

Chi-squared distribution

Definition

Definition

Let Z_1,\ldots,Z_r be iid N(0, 1) random variables. The chi-squared distribution with r degrees of freedom is the distribution \chi^2_r \sim Z^2_1+...+Z^2_r

Chi-squared distribution

Pdf characterization

Theorem

The \chi^2_r distribution is equivalent to a Gamma distribution \chi^2_r \sim \Gamma(r/2, 1/2) Therefore the pdf of \chi^2_r can be written in closed form as f_{\chi^2_r}(x)=\frac{x^{(r/2)-1} \, e^{-x/2}}{\Gamma(r/2) 2^{r/2}} \,, \quad x>0

Chi-squared distribution

Plots of chi-squared pdf for different choices of r

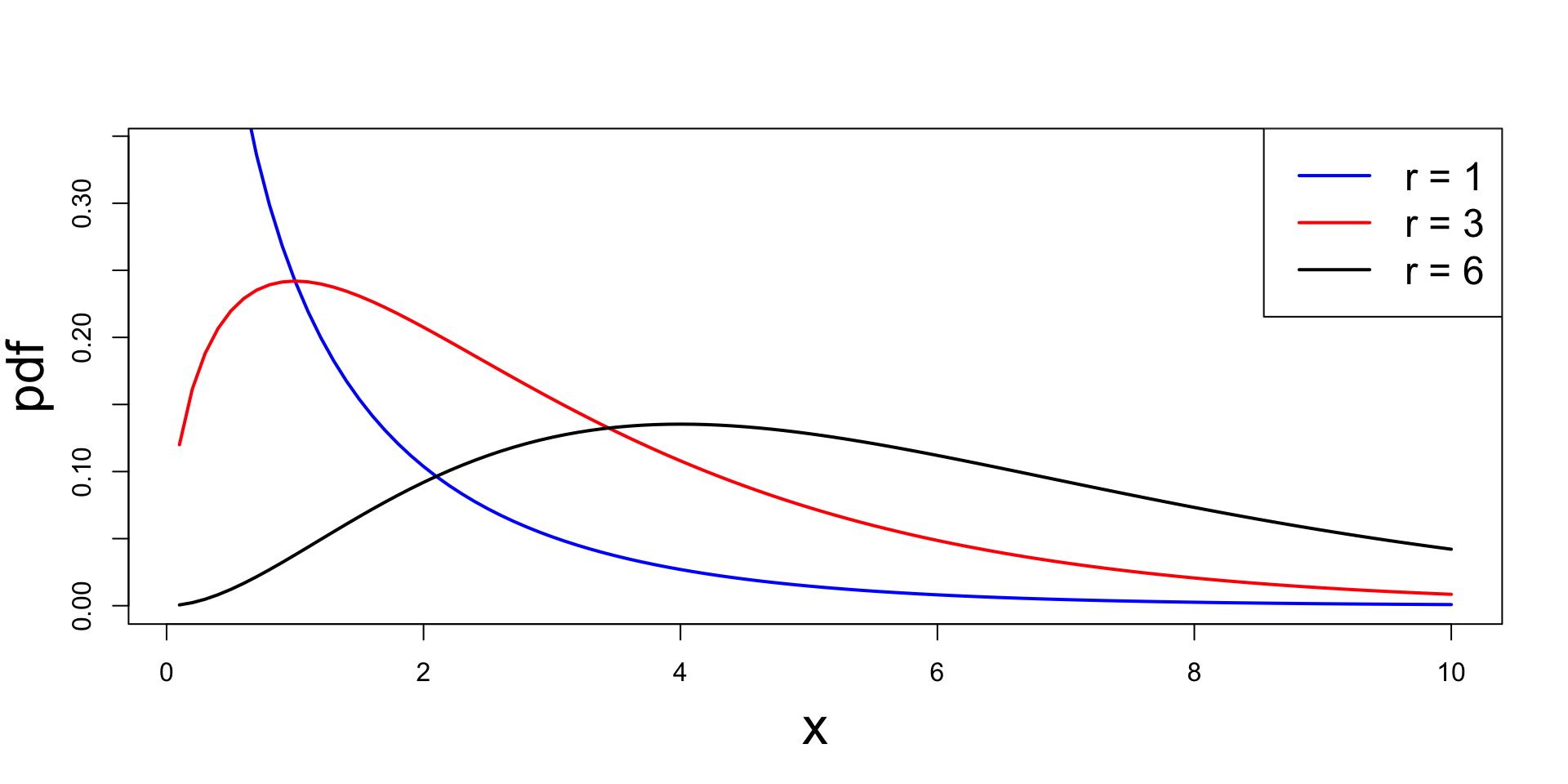
Chi-squared distribution

Proof of Theorem

• We start with case the r=1
• Need to prove that \chi^2_1 \sim \Gamma(1/2, 1/2)
• Therefore we need to show that the pdf of \chi^2_1 is f_{\chi^2_1}(x)=\frac{x^{-1/2} \, e^{-x/2}}{\Gamma(1/2) 2^{1/2}} \,, \quad x>0

Chi-squared distribution

Proof of Theorem

• To this end, notice that by definition \chi^2_1 \sim Z^2 \,, \qquad Z \sim N(0,1)
• Hence, for x>0 we can compute cdf via \begin{align*} F_{\chi^2_1}(x) & = P(\chi^2_1 \leq x) \\ & = P(Z^2 \leq x ) \\ & = P(- \sqrt{x} \leq Z \leq \sqrt{x} ) \\ & = 2 P (0 \leq Z \leq \sqrt{x}) \end{align*} where in the last equality we used symmetry of Z around x=0

Chi-squared distribution

Proof of Theorem

• Recalling the definition of standard normal pdf we get \begin{align*} F_{\chi^2_1}(x) & = 2 P (0 \leq Z \leq \sqrt{x}) \\ & = 2 \frac{1}{\sqrt{2\pi}} \int_0^{\sqrt{x}} e^{-t^2/2} \, dt \\ & = 2 \frac{1}{\sqrt{2\pi}} G( \sqrt{x} ) \end{align*} where we set G(x) := \int_0^{x} e^{-t^2/2} \, dt

Chi-squared distribution

Proof of Theorem

• We can now compute pdf of \chi_1^2 by differentiating the cdf

• By the Fundamental Theorem of Calculus we have G'(x) = \frac{d}{dx} \left( \int_0^{x} e^{-t^2/2} \, dt \right) = e^{-x^2/2} \quad \implies \quad G'(\sqrt{x}) = e^{-x/2}

• Chain rule yields \begin{align*} f_{\chi^2_1}(x) & = \frac{d}{dx} F_{\chi^2_1}(x) = \frac{d}{dx} \left( 2 \frac{1}{\sqrt{2\pi}} G( \sqrt{x} ) \right) \\ & = 2 \frac{1}{\sqrt{2\pi}} G'( \sqrt{x} ) \frac{x^{-1/2}}{2} = \frac{x^{-1/2} e^{-x/2}}{2^{1/2} \sqrt{\pi}} \end{align*}

Chi-squared distribution

Proof of Theorem

• It is well known that \Gamma(1/2) = \sqrt{\pi}
• Hence we conclude f_{\chi^2_1}(x) = \frac{x^{-1/2} e^{-x/2}}{2^{1/2} \sqrt{pi}} = \frac{x^{-1/2} e^{-x/2}}{2^{1/2} \Gamma(1/2)}
• This shows \chi_1^2 \sim \Gamma(1/2,1/2)

Chi-squared distribution

Proof of Theorem

• Now consider the case r \geq 2. We need to prove that \chi^2_r \sim \Gamma(r/2, 1/2)

• By definition \chi^2_r \sim Z^2_1 + \ldots + Z^2_r \,, \qquad \chi^2_1 \sim Z_1^2

• It follows that a \chi^2_r random variable can be constructed as \chi^2_r = \sum_{i=1}^r X_i, \qquad X_i \sim \chi^2_1

• By the Theorem in Slide 80 in Lecture 2 we have Z_1,\ldots,Z_r \,\,\, \text{iid} \quad \implies \quad Z_1^2,\ldots,Z_r^2 \,\,\, \text{iid} \quad \implies \quad X_1,\ldots,X_r \,\,\, \text{iid}

Chi-squared distribution

Proof of Theorem

• Therefore \chi^2_r = \sum_{i=1}^r X_i \,, \qquad X_i \sim \chi_1^2 \,\, \,\text{ iid}

• Recall that the MGF of sum of iid random variables is the product of the MGFs - see Theorem in Slide 81 of Lecture 2

• Thus the MGF of \chi^2_r can be calculated as M_{\chi_r^2}(t) = \prod_{i=1}^r M_{X_i} (t) = \left[M_{\chi^2_1}(t) \right]^r

Chi-squared distribution

Proof of Theorem

• We have proven that \chi_1^2 \sim \Gamma(1/2,1/2)

• In Lecture 1 we have also computed that Y \sim \Gamma(\alpha,\beta) \qquad \implies \qquad M_Y(t) = \frac{\beta^\alpha}{(\beta - t)^\alpha}

• Hence M_{\chi_1^2}(t) = \frac{2^{-1/2}}{(1/2 - t)^{1/2}}

Chi-squared distribution

Proof of Theorem

• Therefore M_{\chi_r^2}(t) = \left[M_{\chi^2_1}(t) \right]^r = \left[ \frac{2^{-1/2}}{ (1/2 - t)^{1/2}} \right]^r = \frac{2^{-r/2}}{(1/2 - t)^{r/2}}

• The above is the MGF of a \Gamma(r/2,1/2)

• Since MGF characterizes a distribution, we conclude our thesis \chi_r^2 \sim \Gamma(r/2,1/2)

Part 4:
Sampling from normal distribution

Sampling from Normal distribution

Sample mean and variance: For a random sample X_1,\ldots,X_n defined by S^2 := \frac{1}{n-1} \sum_{i=1}^n \left( X_i - \overline{X} \right)^2 \,, \qquad \overline{X} := \frac{1}{n} \sum_{i=1}^n X_i

Question

Assume the sample is normal X_i \sim N(\mu,\sigma^2) \,, \quad \forall \, i = 1 , \ldots, n What are the distributions of \overline{X} and S^2?

Properties of Sample Mean and Variance

Theorem

Let X_1,\ldots,X_n be a random sample from N(\mu,\sigma^2). Then

• \overline{X} and S^2 are independent random variables
• \overline{X} and S^2 are distributed as follows \overline{X} \sim N(\mu,\sigma^2/n) \,, \qquad \frac{(n-1)S^2}{\sigma^2} \sim \chi_{n-1}^2

Properties of Sample Mean and Variance

Proof of Theorem

• To prove independence of \overline{X} and S^2 we make use of the following lemma
• Proof of this Lemma is technical and omitted
• For a proof see Lemma 5.3.3 in [1]

Lemma

Let X and Y be normal random variables. Then X \text{ and } Y \text{ independent } \quad \iff \quad {\rm Cov}(X,Y) = 0

Properties of Sample Mean and Variance

Proof of Theorem

• We now apply the Lemma to X_i - \overline X and \overline{X}

• Note that X_i - \overline{X} and \overline{X} are normally distributed, being sums of iid normals

• Therefore we can apply the Lemma

• To this end, recall that {\rm Var}[\overline X] = \sigma^2/n

• Also note that, by independence of X_1,\ldots,X_n {\rm Cov}(X_i,X_j) = \begin{cases} {\rm Var}[X_i] & \text{ if } \, i = j \\ 0 & \text{ if } \, i \neq j \\ \end{cases}

Properties of Sample Mean and Variance

Proof of Theorem

• Using bilinearity of covariance (i.e. linearity in both arguments) \begin{align*} {\rm Cov}(X_i - \overline X, \overline X) & = {\rm Cov}(X_i,\overline{X}) - {\rm Cov}(\overline X,\overline{X}) \\ & = \frac{1}{n} \sum_{j=1}^n {\rm Cov}(X_i,X_j) - {\rm Var}[\overline X] \\ & = \frac{1}{n} {\rm Var}[X_i] - {\rm Var}[\overline X] \\ & = \frac{1}{n} \sigma^2 - \frac{\sigma^2}{n} = 0 \end{align*}

• By the Lemma we infer independence of X_i - \overline X and \overline X

Properties of Sample Mean and Variance

Proof of Theorem

• We have shown X_i - \overline X \quad \text{and} \quad \overline X \quad \text{independent}

• By the Theorem in Slide 80 in Lecture 2 we hence have (X_i - \overline X)^2 \quad \text{and} \quad \overline X \quad \text{independent}

• By the same Theorem we also get \sum_{i=1}^n (X_i - \overline X)^2 = (n-1)S^2 \quad \text{and} \quad \overline X \quad \text{independent}

• Again the same Theorem, finally implies independence of S^2 and \overline X

Properties of Sample Mean and Variance

Proof of Theorem

• We now want to show that \overline{X} \sim N(\mu,\sigma^2/n)

• We are assuming that X_1,\ldots,X_n are iid with {\rm I\kern-.3em E}[X_i] = \mu \,, \qquad {\rm Var}[X_i] = \sigma^2

• We have already seen in Slides 15 and 17 that, in this case, {\rm I\kern-.3em E}[\overline X] = \mu \,, \quad {\rm Var}[\overline{X}] = \frac{\sigma^2}{n}

• Sum of independent normals is normal (see Theorem in slide 82 in Lecture 2)

• Therefore \overline{X} is normal, with mean \mu and variance \sigma^2/n

Properties of Sample Mean and Variance

Proof of Theorem

• We are left to prove that \frac{(n-1)S^2}{\sigma^2} \sim \chi_{n-1}^2
  • This is somewhat technical and we don’t actually prove it
  • For a proof see Theorem 5.3.1 in [1]
  • We however want to provide some intuition on why it holds
• Recall that the chi-squared distribution with r degrees of freedom is \chi_r^2 \sim Z_1^2 + \ldots + Z_r^2 with Z_i iid and N(0,1)

Properties of Sample Mean and Variance

Proof of Theorem

• By definition of S^2 we have \frac{(n-1)S^2}{\sigma^2} = \sum_{i=1}^n \frac{(X_i - \overline X)^2}{\sigma^2}

• If we replace the sample mean \overline X with the actual mean \mu we get the approximation \frac{(n-1)S^2}{\sigma^2} = \sum_{i=1}^n \frac{(X_i - \overline X)^2}{\sigma^2} \approx \sum_{i=1}^n \frac{(X_i - \mu)^2}{\sigma^2}

Properties of Sample Mean and Variance

Proof of Theorem

• Since X_i \sim N(\mu,\sigma^2), we have that Z_i := \frac{X_i - \mu}{\sigma} \sim N(0,1)

• Therefore \frac{(n-1)S^2}{\sigma^2} \approx \sum_{i=1}^n \frac{(X_i - \mu)^2}{\sigma^2} = \sum_{i=1}^n Z_i^2 \sim \chi_n^2

• This is just an approximation: Replacing \mu with \overline X loses of 1 degree of freedom \frac{(n-1)S^2}{\sigma^2} \sim \chi_{n-1}^2

Part 5:
t-distribution

Estimating the Mean

Problem

We want to estimate the mean \mu of a normal population

What to do?

• We can collect normal samples X_1, \ldots, X_n with X_i \sim N(\mu,\sigma^2)

• We then compute the sample mean \overline X := \frac{1}{n} \sum_{i=1}^n X_i

• We know that {\rm I\kern-.3em E}[\overline X] = \mu

Estimating the Mean

Therefore we expect \overline X to approximate \mu

Question

How good is this approximation? How to quantify it?

Answer: We could look at the Test Statistic T := \frac{\overline{X}-\mu}{\sigma/\sqrt{n}}

• We know that T \sim N(0,1) – Because \overline X \sim N(\mu,\sigma^2/n) as seen in Slide 48
• If \sigma is known, then the only unknown in T is \mu
• Therefore T can be used to estimate \mu

Estimating the Mean

Question

In what way can we use the test statistic T = \frac{\overline{X}-\mu}{\sigma/\sqrt{n}} to estimate \mu?

Answer: Hypothesis testing

Estimating the Mean

Hypothesis testing algorithm

• We suppose that \mu=\mu_0 for some guessed \mu_0
• \mu_0 is called null hypothesis
• Using the data collected \mathbf{X}= (X_1,\ldots,X_n) we compute t := \frac{\overline{X}-\mu_0}{\sigma/\sqrt{n}} \,, \qquad \overline{X} = \frac{1}{n} \sum_{i=1}^n X_i
• Since T \sim N(0,1), we can compute the probability of T being close to t p := P(T \approx t)

Estimating the Mean

Hypothesis testing algorithm

Given the value p := P(T \approx t) we have 2 options:

• p is small \quad \implies \quad reject \mu_0
  • p small means it is unlikely to observe such value of t
  • Recall that t depends on the data \mathbf{X} and our guess \mu_0
  • We conclude that our guess must be wrong \quad \implies \quad \mu \neq \mu_0
• p is large \quad \implies \quad do not reject \mu_0
  • p large means that t happens with reasonably high probability
  • There is no reason to believe our guess \mu_0 was wrong
  • But we also do not have sufficient reason to believe \mu_0 was correct

Estimating the Mean

Important

The key step in the Hypothesis Testing Algorithm is computing p = P(T \approx t) This is only possible if we know the distribution of T = \frac{\overline{X}-\mu}{\sigma/\sqrt{n}} If we assume that the variance \sigma^2 is known, then T \sim N(0,1) and p is easily computed

Estimating the Mean

Unknown variance

Problem

In general the population variance \sigma^2 is unknown. What to do?

Idea: We can replace \sigma^2 by the sample variance S^2 = \frac{\sum_{i=1}^n X_i^2 - n \overline{X}^2}{n-1} The new test statistic is hence T := \frac{\overline{X}-\mu}{S/\sqrt{n}}

Estimating the Mean

Question

What is the distribution of

T := \frac{\overline{X}-\mu}{S/\sqrt{n}} \qquad ?

Answer: T has t-distribution with n-1 degrees of freedom

• This is also known as Student’s t-distribution
• Student was the pen name under which W.S. Gosset was publishing his research
• He was head brewer at Guinness, at the time the largest brewery in the world!
• Used t-distribution to study chemical properties of barley from low samples [2] (see original paper )

t-distribution

Definition

Definition

A random variable T has Student’s t-distribution with p degrees of freedom, denoted by T \sim t_p \,, if the pdf of T is f_T(t) = \frac{\Gamma \left( \frac{p+1}{2} \right) }{\Gamma \left( \frac{p}{2} \right)} \, \frac{1}{(p\pi)^{1/2}} \, \frac{ 1 }{ (1 + t^2/p)^{(p+1)/2} } \,, \qquad t \in \mathbb{R}

t-distribution

Characterization

Theorem

Let U \sim N(0,1) and V \sim \chi_p^2 be independent. The random variable T := \frac{U}{\sqrt{V/p}} has t-distribution with p degrees of freedom, that is, T \sim t_{p}

Proof: Given as exercise in Homework assignments

Distribution of t-statistic

As a consequence of the Theorem in previous slide we obtain:

Theorem

Let X_1,\ldots,X_n be a random sample from N(\mu,\sigma^2). Then the random variable T = \frac{\overline{X}-\mu}{S/\sqrt{n}} has t-distribution with n-1 degrees of freedom T \sim t_{n-1}

Distribution of t-statistic

Proof of Theorem

• Since X_1,\ldots,X_n is random sample from N(\mu,\sigma^2), we have shown that \overline{X} \sim N(\mu, \sigma^2/n)

• Therefore we can renormalize and obtain U := \frac{ \overline{X} - \mu }{ \sigma/\sqrt{n} } \sim N(0,1)

Distribution of t-statistic

Proof of Theorem

• We have also shown that V := \frac{ (n-1) S^2 }{ \sigma^2 } \sim \chi_{n-1}^2

• Finally, we can rewrite T as T = \frac{\overline{X}-\mu}{S/\sqrt{n}} = \frac{U}{ \sqrt{V/(n-1)} }

• By the Theorem in Slide 66 we conclude that T \sim t_{n-1}

Properties of t-distribution

Proposition: Expectation and Variance of t-distribution

Suppose that T \sim t_p. We have:

• If p>1 then {\rm I\kern-.3em E}[T] = 0
• If p>2 then {\rm Var}[T] = \frac{p}{p-2}

Notes:

• We have to assume p>1 otherwise {\rm I\kern-.3em E}[T] = \infty for p=1
• We have to assume p>2 otherwise {\rm Var}[T] = \infty for p=1,2
• {\rm I\kern-.3em E}[T] = 0 follows trivially from symmetry of the pdf f_T(t) around t=0
• Computing {\rm Var}[T] is quite involved, and we skip it

t-distribution

Comparison with Standard Normal

The t_p distribution generalizes standard normal N(0,1):

• t_p it is symmetric around zero and bell-shaped, like N(0,1)
• t_p has heavier tails compared to N(0,1)
• While the variance of N(0,1) is 1, the variance of t_p is \frac{p}{p-2}
• We have that t_p \to N(0,1) \quad \text{as} \quad p \to \infty

t-distribution

Plots: Comparison with Standard Normal

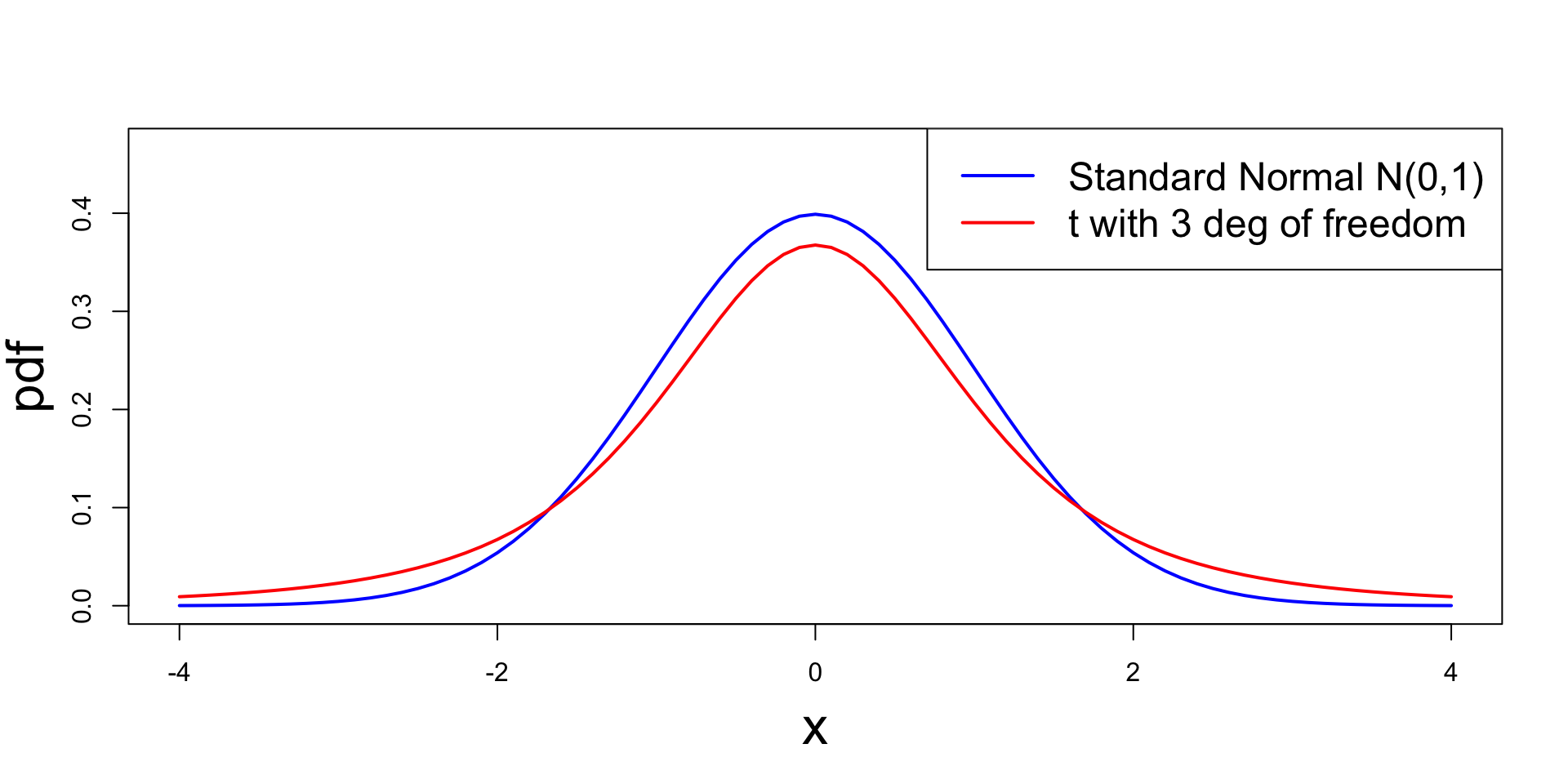
Part 6:
Hypothesis testing

Hypothesis testing

Definition of Hypothesis

• Idea:
  • Interested in knowing a population parameter \theta
  • \theta cannot be measured directly
  • We can sample the population and draw conclusions on \theta
  • Such conclusions are hypotheses

Definition

A hypothesis is a statement about a population parameter

Hypothesis testing

Complementary hypotheses

• Two hypotheses are complementary if exactly one of them can be true

• Complementary hypotheses are called:

  • H_0 the null hypothesis
  • H_1 the alternative hypothesis

• Goal: Find a way to decide which between H_0 and H_1 is true

Hypothesis testing

How to model hypotheses

We denote by:

• \theta a population parameter
• \Theta the space of all population parameters

For \Theta_0 \subset \Theta we define the associated null and alternative hypotheses as \begin{align*} H_0 \colon & \theta \in \Theta_0 & \qquad \text{ null hypothesis} \\ H_1 \colon & \theta \in \Theta_0^c & \qquad \text{ alternative hypothesis} \end{align*}

Hypothesis testing

Definition of Hypothesis test

Definition

A hypothesis test is a rule to decide:

• For which sample values we decide to accept H_0 as true
• For which sample values we reject H_0 and accept H_1 as true

Hypothesis testing

Acceptance and Critical regions

The sample space is partitioned into two regions:

• Acceptance region: For samples \mathbf{X} in this region we accept H_0
• Critical region: For samples \mathbf{X} in this region we reject H_0

In most cases: Critical region is defined in terms of a statistic W(\mathbf{X})

Example: We could decide to reject H_0 if W(\mathbf{X}) \in R with R \subset \mathbb{R} some rejection region

Hypothesis testing

One-sided vs Two-sided Tests

Let \theta be one dimensional parameter. A hypothesis test is:

• One-sided if the null hypotheses are of the form H_0 \colon \theta \leq \theta_0 \qquad \text{ or } \qquad H_0 \colon \theta \geq \theta_0 with corresponding one-sided alternative hypotheses H_1 \colon \theta > \theta_0 \qquad \text{ or } \qquad H_1 \colon \theta < \theta_0

• Two-sided if the null and alternative hypotheses are of the form H_0 \colon \theta = \theta_0 \qquad \text{ and } \qquad H_1 \colon \theta \neq \theta_0

Hypothesis testing

Philosophical issues

• H_0 is usually a conservative hypothesis
• If a test indicates to reject H_0, people do that happily and accept H_1
• If a test indicates to accept H_0 there are issues:
  • Some people like to reject H_1 and accept H_0
  • Some people like to reject H_1, but do not believe fully in H_0. They would like to reject H_0, but do not have enough evidence to do so
• Our position: We do not care, and we either
  • decide in favor of H_0 - or accept H_0
  • decide in favor of H_1 - or accept H_1

Hypothesis testing

Example 1 - Two-seded test

The University of Cottingham Road wants to advertise its MBA Program: \text{ MBA } = \text{ higher salary }

• Is this a true or false statement?

• The University has only access to incomplete data (could not ask all former students). Need hypothesis testing

• \theta = average change in salary after completing the MBA program

  • Null hypothesis: There is no change \,\, \implies \,\, \theta=0
  • Alternative hypothesis: There is a change \,\, \implies \,\, \theta \neq 0

Hypothesis test: \qquad \quad H_0 \colon \theta = 0 \,, \qquad H_1 \colon \theta \neq 0

Hypothesis testing

Example 2 - One-sided test

Manager at a Computer Factory wants to know the proportion of defective components produced

• Testing is expensive and they can only test a limited sample
• \theta = proportion of defective components
• Manager is happy if \theta is less than some \theta_0
• The decision is between:
  • Null hypothesis: Defective components less than \theta_0 \,\, \implies \,\, \theta < \theta_0
  • Alternative hypothesis: Defective components more than \theta_0 \,\, \implies \,\, \theta \geq \theta_0

Hypothesis test: \qquad \quad H_0 \colon \theta < \theta_0 \,, \qquad H_1 \colon \theta \geq \theta_0

References

[1]

Casella, George, Berger, Roger L., Statistical inference, second edition, Brooks/Cole, 2002.

[2]

Gosset (Student), W.S., The probable error of a mean, Biometrika. 6 (1908) 1–25.